非協調システムとゲーム理論:

近年，日本の未来社会として提唱されるスマート社会への注目が集まっている．文献[1]では，スマート社会の実現に向け，電力システムや交通システムを人工知能により制御することで社会価値を増大させる動きが活発になっていると述べる．所有者が異なる複数の人工知能を統合制御することは困難であるため，サブシステムに搭載された人工知能間で協調・連携してシステムを分散制御する仕組みの整備が必要があると文献[1] は主張する．文献[1]が提唱するシステムの設計は複数の意思決定者を含んだマルチエージェントシステム(MAS) の設計・制御と解釈できる．MAS を制御するためにゲーム理論の考えを用いる方法が注目されており，システム工学とゲーム理論両方の観点から盛んに研究が進められている[2][3][4]．現実社会のシステムは時間とともに状態が慣性を有しながら変化する動的なシステムであることから，静的な従来のゲーム理論を状況に合わせて適切に拡張していくことが課題となる．

ゲーム理論の中でも，ゲームを構成するエージェント同士の利害関係や選好が異なり，エージェント同士が協力せずに自分の利益のために行動する状況を扱った非協力ゲーム[5]は，協調システムでは扱えなかった，エージェント同士が協力関係にない現実社会の状況をモデル化する方法として期待される．時々刻々と変化する現実社会をモデル化するには，非協力ゲームの考えを動的なシステムに落とし込み，システムの結果や制御方法について考察を行うことが求められる．本論文では，現実社会をモデル化するために非協力ゲームの考えを取り入れた動的なシステムのことを非協調システムを呼ぶ．

Nash 均衡の安定化

非協力ゲームの重要な均衡解の1 つとして，Nash 均衡があり，この概念は非協調システムにも適用される．非協調システムにおいて，エージェントは満足度を表す効用で特徴づけられる．利己的なエージェントは，自分のもつ効用を増加させるため，効用の説明変数であるエージェント自身の状態を変化させる．Nash均衡を扱う動的システムにおいて，エージェントのダイナミクスは，エージェントが得られる情報やエージェントの戦略などによって様々なものが考案されている[6][7][8]．これらの動的システムにおいて，Nash 均衡は各々のエージェントが自分の状態を変える誘因がない平衡状態であり，エージェントにとっては最善を尽くしたときの結果といえる．もし，あるNash 均衡がシステム全体としても望ましい結果であるならば，状態がこの望ましいNash 均衡に収束することが求められる．Nash 均衡が平衡点であっても安定であるとは限らず，ゲームの結果として状態が望ましいNash 均衡に収束せず，他の平衡点に収束する場合，状態が発散する場合がありうる．現実に即した非協調システムのモデルを考える際，情報の不完全性が問題となる．古典的なゲーム理論では，各エージェントは相手の行動や自分の効用関数の情報が手に入ることを前提に，最適反応の概念を用いて，エージェントが行動を選択し，効用関数を向上させているが，このシステムは極めて理想的で現実とかけ離れているという批判がある．一方，エージェントが効用関数を知らずとも，現在のシステムの状態またはその近傍に対する効用を知っていれば可能な，自分の効用を向上するを状態変化の方法を文献[9] では提案しており，この手法をpayoff-based と呼んでいる．payoff-based の手法では効用関数の勾配に着目するが，効用関数の勾配を用いたシステムの状態変化のモデリングを提案する研究は，文献[9][10][11][12][13] 等数多く行われている．

情報の提示によるエージェントの行動変化

このような，非協力ゲームを活用したMAS である非協調システムのNash 均衡を収束，安定化する方法は，システムを全体が望ましいように制御することを望むシステム管理者がインセンティブなどによりエージェントの効用関数の構造を変化させる方法などが提案されている[14]．この研究は，システム管理者がエージェントに対し補助金などの金銭的なインセンティブを用いることが背景となっている．しかし，金銭的なインセンティブによる方法は，費用がかかるなどの問題点がある．また，近年ではナッジ理論[15][16] のように，エージェントに罰則やインセンティブといった手段を用いずに，新たな気づきを与えることで行動変化を起こす取り組みが行われている．ナッジ理論の考えを非協調システムに当てはめる．新たな気づきとは，システム管理者がエージェントに対し新たな情報を示すことである．これにより，エージェントの効用関数を変えずに，エージェントの行動を表すダイナミクスを変え，Nash 均衡を安定化させることができる．エージェントが持つ，効用関数の構造についての情報や，他者の状態の情報が不完全である場合にナッジ理論の考えは有効である．

インパルス型ハイブリッドシステム

本論文では効用関数を変化させず，エージェントの利己的な行動を制限せずにシステムを安定化する手法を提案する．エージェントが自分の効用関数の全体像についての情報が得られない状況において，非協調システム全体を制御するシステム管理者は断続的に効用に関する情報を提示する．エージェントは新たに入手した情報に基づき，状態変化の方法，すなわちダイナミクスを変更することが可能となる．このダイナミクスは，状態が連続的に変化する中，断続的に離散的な状態変化が発生するインパルス型ハイブリッドシステム(Impulsive Dynamical Systems)[17] として表すことができる．インパルス型ハイブリッドシステムで表す詳細な理由は第2 章で述べる．インパルス型ハイブリッドシステムは，リセットシステム[18] とも呼ばれる．インパルス型ハイブリッドシステムとして扱われる対象は，予防接種による感染症の予防[19]，害虫駆除問題[20]，飛行制御[18]，合意形成[21] 等多くある．[21] ではエージェントの持つ情報が不完全である状況のシステムを扱い，エージェントは断続的に入手できる新たな情報によってダイナミクスを変化させ，状態の離散的な変化を起こす．以降，ハイブリッドシステムと述べた場合はインパルス型ハイブリッドシステムのことを指す．

研究目的

非協調システムのNash 均衡を安定化するため，システムを制御するシステム管理者が部分的な効用情報しか知らないエージェントに対し新たな効用情報を提示し，エージェントが自発的に行動を変化させる手法を提案する．ゲーム 理論とハイブリッドシステムの知見を用いて問題設定を行う．問題設定の下で，不安定なNash 均衡を，シス テム管理者による効用情報の提示で安定化させる適切な情報提供のタイミングを求める．そのため，非協調シ ステムの枠組みの中でハイブリッドシステムが安定である条件を解析する．

問題設定

エージェントがシステム管理者から情報を受け取る前後でエージェントが持つ情報と，それぞれの場面での エージェントの状態変化について問題設定を行う．

はじめに，エージェントがシステム管理者から情報を提示されていないときのダイナミクスを設定する．エージェントは自分の状態を知っており，自由に自分の状態を選択できる．効用の情報については，状態が絶えず変化するシステムの下で状態の選択をしなければならない状況を鑑みて，自分の効用関数の全体像がわからず，現在の状態の近傍に対するの効用の構造しか把握できないと仮定する．このとき，エージェントが選択できる最善の選択は自分の効用関数の自分の状態軸方向の勾配，すなわち疑似勾配[14]に応じて状態を連続的に変化させることである．定式化すると，状態$x_i$の速度が疑似勾配となる(図1)．ここで，$x_i$はエージェント$i(1,2,\dots, n)$を表す状態，$x$は全エージェントの状態を表すベクトル量，$J_i(x(t))$はエージェント$i$の効用関数を表す．

一方，システム管理者はシステム全体を把握できると想定し，各エージェントの効用関数の全体像を得られることから，それぞれのエージェントに効用関数の情報を提示できるとする．各エージェントにとって有益となる効用情報の1 つは，効用関数$J_i(x)$に他エージェントの現在の状態$x_{-i}(t)$ を代入した$x_i$の関数である．ここで，$x_{-i}$は$x_i$以外の全ての状態を表す．エージェント$i$が受け取る効用関数は$J_i(x_i, x_{-i}(t))$(図2の赤線)．エージェントは情報提供を受けたとき，現在のシステムの状態において自分にとって最善な行動を選択し，即座に自分の状態を変化させることで効用を向上させることができる．この行動選択は，従来の静的な非協力ゲームで用いられる最適反応(Best Response, BR) にあたる．つまり，他エージェントの現在の状態の下，自分の効用関数が最大となるような自分の状態を計算し，次の瞬間に状態を離散的に変化させる戦略である．

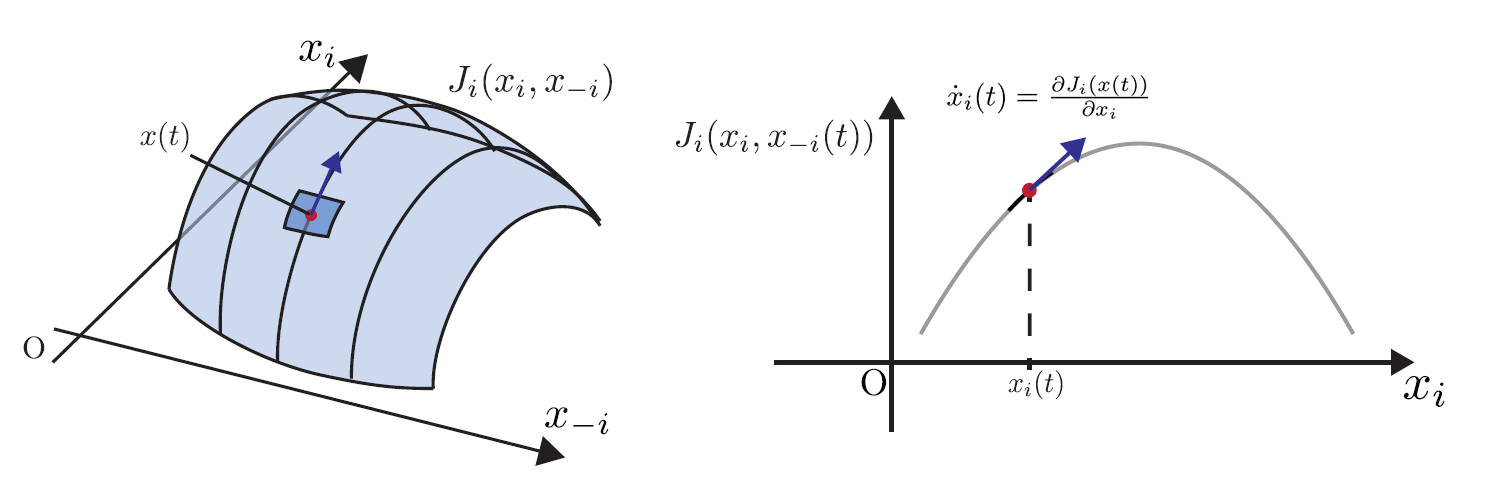図1: エージェントが把握できる効用情報(濃青部)と疑似勾配(青矢印)

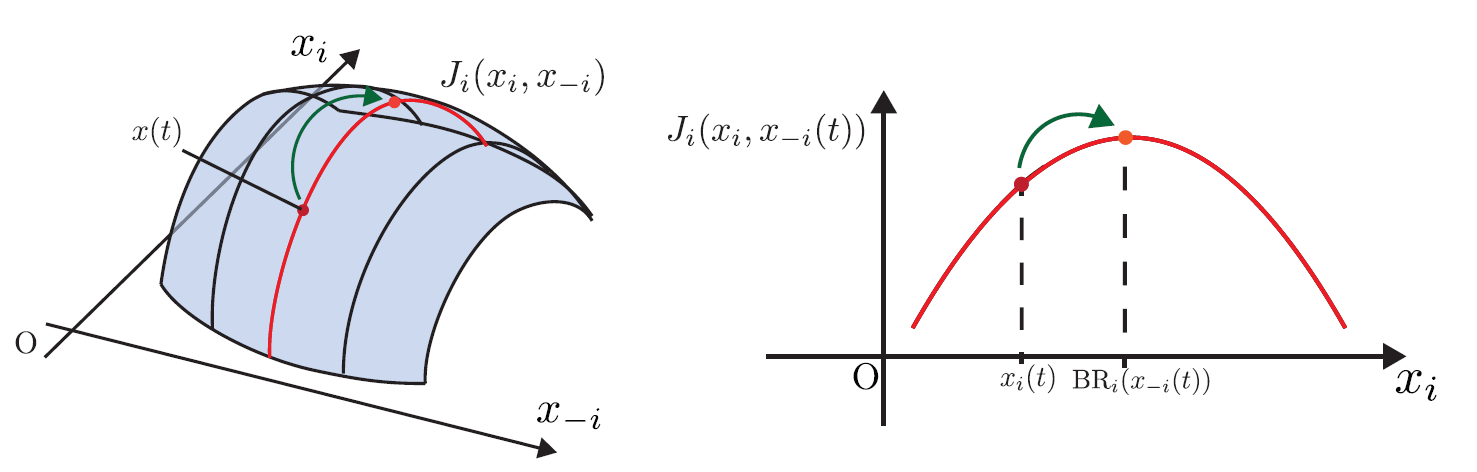図2: システム管理者が出す効用情報$J_i(x_i, x_{-i}(t))$(赤線部) と最適反応(橙点)

エージェントの状態変化は，連続的な変化と離散的な変化が混在したインパルス型ハイブリッドシステム(Impulsive Dynamical Systems)で表す． $$\large \dot{x}(t)=A x(t),\quad (t,x(t)) \not \in \mathcal{S}, \quad x(0)=x_0 \label{cns} $$ $$\large x(t^+)=Bx(t),\quad (t,x(t)) \in \mathcal{S} \label{dns} $$ ここで，$A$,$B$は効用関数の係数から，疑似勾配・最適反応に従い決定する行列である． システム管理者が効用情報を提示するタイミングを時刻と状態の集合$\mathcal{S}$で表す． 本論文では，効用提示の条件が時刻で定められ，周期$\Delta t$で発生する時間依存のハイブリッドシステムと， エージェント数が3の場合について，状態$x(t)$が3次元空間上の平面に到達したときに効用提示を行う状態依存のハイブリッドシステムを扱う．

研究結果

システムの安定性を解析し，Nash 均衡が安定であるような，効用情報を提示する条件集合と効用関数の条件を導出した．その結果により，不安定なNash均衡を安定化できる事例と条件集合の求め方を示した．

時間依存ハイブリッドシステムにおいて，安定性行列$e^{A\Delta t}B$の固有値の絶対値に依存する．この行列は，$k$回目と$k+1$回目に効用情報を提示する直前の2つの状態の関係を表したものである．この結果を用い，不安定な連続時間ダイナミクスを安定化するような$\Delta t$を求める問題を解析した．特に，エージェント数が2 つの場合において，不安定なNash 均衡を安定化することは不可能であることがわかった． また，効用関数の係数が安定化問題に与える影響について述べた．各エージェントにおいて，効用関数の断面の形状(図2の赤線部)を特徴づける係数が全て等しいと，システムが安定化不可能であることを示し，定理の解釈を図形的な側面から概説した．このように，効用関数の条件によっては，システムを安定化できるような$\Delta t$が存在しない．この性質は，連続的な変化・離散的な変化ともエージェントは利己的に行動する非協調システム特有の性質といえる．

状態依存ハイブリッドシステムにおいても同様に安定条件と安定化できる事例を示した．また，時間依存ハイブリッドシステムと安定条件の比較を行った． 状態依存ハイブリッドシステムは，状態が条件集合を表す平面に必ずしも到達するとは限らないため，状態が 平面に無限回，かつ周期的に到達するための条件を示し，その条件が成り立つことを前提とした安定 条件を導出した．本論文で提案する条件を満たせば，同じ周期の時間依存ハイブリッドシステムに比べ， $e^{A\Delta t}B$の固有値の絶対値についての条件を緩和することができる．これは，状態依存ハイブリッドシステムは時間依存のシステムとは異なり，状態のジャンプが発生する箇所を限定できることが理由と考えられる．