線形周期システムの適応安定化
研究背景・先行研究
周期システム
衛星システムの周期軌道,産業プロセスシステムにおける化学反応系,通信システムにおける情報伝達機構,経済システムにおける景気循環など,周期的な現象はさまざまな分野で観察される[1-4]. 周期システムの研究は19世紀の微分方程式に対する考察から始まり,その解析手法はフロケ理論として整備されている.20世紀後半には工学的応用の面から焦点が当てられ,多くの研究者の関心を寄せてきた.特に制御工学の分野では,フロケ理論の拡張[5,6],非線形システムに埋め込まれた不安定な周期軌道を安定化する手法[7]などが報告されている.
特に,周期システムが周期解をもつとき,この周期解の安定性を解析する手法が,ポアンカレによって提案された[8].この手法では,周期解の状態を離散的に取り出してシステムを定義することで,周期システムのもつ周期解の安定性を解析する問題を,離散システムのもつ固定点の安定性を解析する問題に帰着させている.文献[9,10]では,周期解の安定性と固定点の安定性が等価であることが,リアプノフの安定論に基づいて示されている.
遅延フィードバック制御手法による周期システムの安定化
周期システムの状態を周期解まわりで安定化する制御器は,遅延フィードバック制御の理論[11,12]に基づいて設計することが有効である.通常の状態フィードバック制御では,現在の状態のみを用いて入力を設計するが,遅延フィードバック制御では,現在の状態に加えて1周期前の状態を用いて入力を構成する.遅延フィードバック制御は,カオスシステムなどの非線形システムに埋め込まれた不安定周期軌道を安定化する手法として用いられる[13].文献[14]では,遅延フィードバック制御によって,周期システムの状態が平衡点周りで安定化できない条件について述べられている.文献[15]では,周期システムに遅延フィードバック制御入力を印加したとき,閉ループ系の安定性を解析する手法について述べられている.
遅延フィードバック制御の手法は,通常の状態フィードバック制御では制御困難なシステムに対して有効となる場合があるが,一方でいくつかの欠点がある.例えば,遅延フィードバック制御で入力を構成した場合,閉ループシステムの状態の軌道を記述する微分方程式は,理論的に解析が困難となる.そのため,設計した制御手法の有用性を,理論的に保証することが同様に困難となる.この問題は,[16]によって提案された,Act-and-Wait遅延フィードバック制御という手法によって解決することができる.この手法では,制御入力を1周期ごとにON,OFF,ON,OFF,...と切り替える形式で設計する. これにより,閉ループシステムの状態の軌道を記述する微分方程式を,理論的に解析することが可能となる.つまり,対象とするシステムの係数行列と制御入力を構成するゲイン行列によって定義される行列(Monodromy行列)の固有値を調べることによって, 状態の軌道を周期ごとに調べることが可能となる.しかし,Act-and-Wait遅延フィードバック制御の実システムへの適用には,多くの課題が残っており,現在も広く研究が進められている.
Act-and-Wait遅延フィードバック制御は,非線形システムに内在する不安定周期軌道を安定化する手法として提案されたが,線形周期システムの周期解の安定化にも適用できる[17].文献[18]では,対象とするシステムの周期の2倍間隔で遅延フィードバック制御入力を印加する手法が提案されている.文献[19]では,制御入力がOFFの時間と安定領域の関係性について言及されている.また,この手法は各時刻において,現在の状態に加えて1周期前の状態の情報を必要とするので,実装の際には十分なメモリ領域を確保する必要があるという問題がある.この問題に対するアプローチとして,[20]では,各周期ごとに状態の情報を1回のみ取得することで制御入力を設計するサンプル値遅延フィードバック制御が提案されている.この手法を拡張し,[21]では,サンプル値Act-and-Wait遅延フィードバック制御が提案されている.
研究目的
周期システムの安定化に遅延フィードバック制御手法が有効であるが,遅延フィードバック制御入力のゲイン行列を解析的に設計することは一般に困難であるという問題があり,ゲイン行列の設計には数値的な方法が採られることが多い.したがって,遅延フィードバック制御手法による周期システムの安定化に関する先行研究において,周期システムが不確かさをもつという条件下でゲイン行列を逐次的に更新してシステムを安定化する適応制御則を設計した研究は少ない.本研究では,不確かさをもつ2次元線形周期システムに対して,Act-and-wait型のサンプル値遅延フィードバック制御入力[21]を印加し,そのゲイン行列を適応的に更新することでシステムを安定化する手法(図1)を提案する.
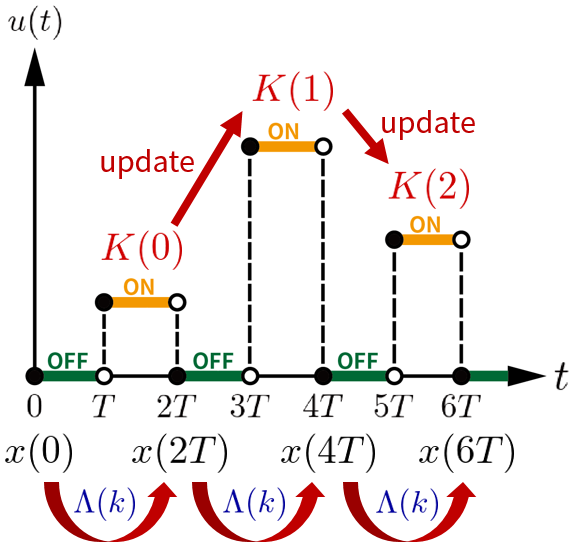 |
| 図1: Input signal of adaptive sampled-data act-and-wait fashioned delayed feedback control |
提案手法
Act-and-wait型のサンプル値遅延フィードバック制御入力を2次元線形周期システムに印加すると,閉ループシステムの状態の遷移を表す離散時間システムが得られる.そして,そのシステムの安定性を解析することで,周期システムの安定性を解析することができる.2次元線形周期システムが不確かさをもつとき,離散時間システムも不確かさをもつため,2次元線形周期システムのもつ不確かさと離散時間システムの不確かさの関係性を調べる.そして,不確かさをもつ離散時間システムに対する適応制御の理論に基づいて,Act-and-wait型のサンプル値遅延フィードバック制御入力[21]の更新則を設計する.提案手法により,離散時間システムが安定化され,2次元線形周期システムが安定化されることをリアプノフの安定性定理によって証明する.数値シミュレーションの結果を,図2--図3に示す.
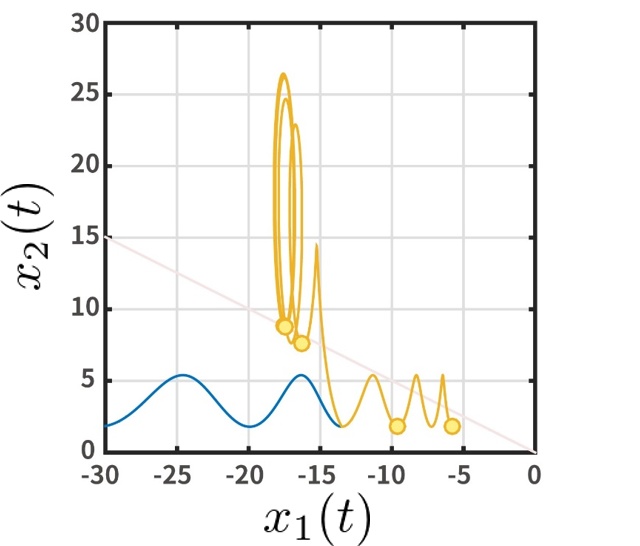 |
| 図2: Phase portrait of linear periodic system stabilized by the proposed method |
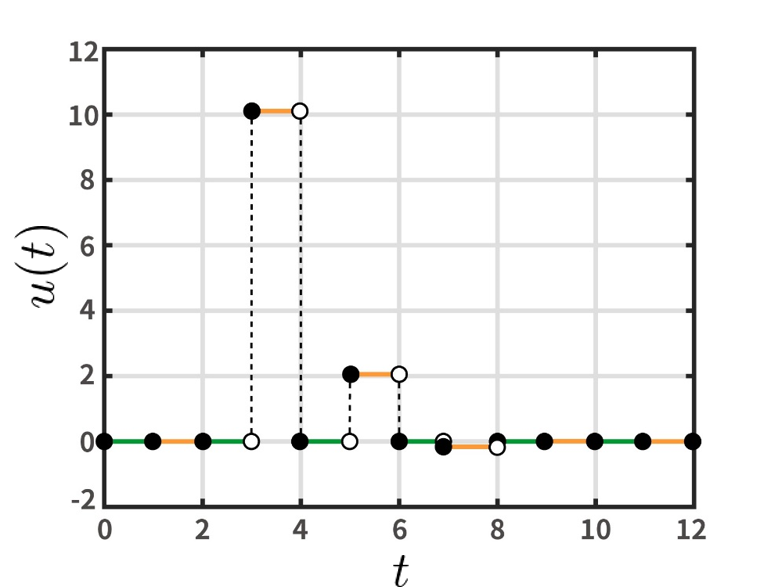 |
| 図3: Control input versus time of the proposed method stabilizing linear periodic system |
今後の方針
本研究における提案手法には,適用できる線形周期システムのクラスが限られているという問題がある.したがって,今後は提案手法をより広いクラスの線形周期システムに適用できるように定理を拡張することが挙げられる.また,非線形システムに不安定な周期軌道が埋め込まれているとき,その軌道周りでシステムを線形化したときの状態のダイナミクスは線形周期システムとして記述されることが知られている.したがって,提案手法を不確かさをもつ非線形システムの安定化制御問題に応用することが考えられる.
参考文献
[1] S. Bittanti and P. Colaneri, Periodic Systems: Filtering and Control, Springer-Verlag, 2009.
[2] M. Pereira, D. Limon, D. Munoz de la Pena, L. Valverde, and T. Alamo, "Periodic economic control of a nonisolated microgrid," IEEE Transactions on Industrial Electronics, vol. 62, no. 8, pp. 5247-5255, 2015.
[3] A. Mukherjee, D. Searson, and M. Willis, "Improved control of a chaotic reaction system using modified delay co-ordinate feedback," Proc. of Asian Control Conference, pp. 571-576, 2009.
[4] E. Garcia, Y. Cao, and W. Casbeer, "Cooperative control with general linear dynamics and limited communication: periodic updates," Proc. of American Control Conference, pp. 3195-3199, 2014.
[5] I. Jikuya and I. Hodaka, "A Floquet-like factorization for linear periodic systems," Proc. of IEEE Conference on Decision and Control, pp. 6432-6437, 2009.
[6] I. Jikuya and I. Hodaka, "Factorizing the monodromy matrix oflinear periodic systems," Proc. of the 19th World CongressThe International Federation of Automatic Control, pp. 11743-11748, 2014.
[7] T. P. Chagas, P. A. Bliman, and K. H. Kienitz, "A new method for stabilizing unstable periodic orbits ofcontinuous-time systems. Application to control of chaos," Proc. of IEEE Conference on Decision and Control, pp. 2146-2151, 2012.
[8] H. K. Khalil, Nonlinear Systems, Prentice Hall, 1996.
[9] W. M. Haddad, S. G. Nersesov, and V. Chellaboina, "A Lyapunov function proof of Poincare’s theorem," Proc. of American Control Conference, vol. 5, pp. 3922-3925, 2002.
[10] A. Leonessa, W. M. Haddad and V. S. Chellaboina, "Nonlinear system stabilization via hierarchical switching control," IEEE Transactions on Automatic Control, vol. 46, no. 1, pp. 17-28, 2001.
[11] K. Pyragas, "Continuous control of chaos by self-controlling feedback," Physics Letters A, vol. 170, pp. 421-428, 1992.
[12] K. Pyragas, "Control of chaos via extended delay feedback," Physics Letters A, vol. 206, pp. 5-6, 1995.
[13] T. Hasegawa and T. Tsubone, "Stabilizing unstable periodic orbits in higher dimensional systems based on stability transformation method," Proc. of IEEE Asia Pacific Conference, pp. 208-211, 2012.
[14] E. W. Hooton and A. Amann, "Analytical limitation for time-delayed feedback control in autonomous systems," Physical Review Letters, vol. 109, pp. 154101, 2012.
[15] C. Shao and J. Sheng, "Stability analysis and control of linear periodic time-delay systems with state-space models based on semi-discretization," Proc. of 2012 UKACC International Conference on Control, pp. 784-788, 2012.
[16] T. Insperger, "Act-and-wait concept for continuous-time control systems with feedback delay," IEEE Transactions on Control Systems Technology, vol. 14, pp. 974-977, 2006.
[17] M. Taib and T. Hayakawa, "Delayed feedback control for linear time-varying periodic systems in act-and-wait fashion," IFAC International Workshop on Periodic Control Systems, pp. 11-16, 2013.
[18] R. Qi, F. Qian, W. Du, X. Yan, and N. Luo, "Stabilizing the unstable periodic orbits via improved delayed feedback control for discrete chaotic systems," Proc. of World Congress on Intelligent Control and Automation, pp. 868-872, 2006.
[19] K. Konishi, H. Kokame, and, N. Hara, "Delayed feedback control based on the act-and-wait concept," An International Journal of Nonlinear Dynamics and Chaos in Engineering Systems, vol. 63, pp. 513-519, 2010.
[20] K. Hirata, "On a design method of sampled-data delayed feedback controller," Proc. of IFAC World Congress, vol. 38, pp. 868-873, 2005.
[21] A. Cetinkaya and T. Hayakawa, "Periodic orbit stabilization through act-and-wait-fashioned sample-data delayed feedback control," Proc. of 54th IEEE Conference on Decision and Control, pp. 1409-1414, 2015.