研究背景と先行研究
ブロードキャスト制御
近年,マルチエージェントシステムの制御が大きな注目を集めている.マルチエージェントシステムの制御の研究は,協調ロボット制御,電力ネットワーク制御,センサネットワーク制御への応用からも重要であることが知られている.多くの研究では,マルチエージェントシステムのエージェント同士の通信により,エージェント全体の目標を達成することを目的としている[1].もし,中央制御器がそれぞれのエージェントに対して適切な入力を送信できるのであれば,システム全体の制御目標を達成させることは簡単である.しかし,中央制御器が一度に送信できる入力の数に制限がある場合,単一かつ単純な入力をすべてのエージェントに送信するブロードキャスト制御の手法を選択するかもしれない.ブロードキャスト制御においては,中央制御器と各エージェントに取り付けられたローカル制御器により,マルチエージェントシステムの制御を行うことを仮定している.
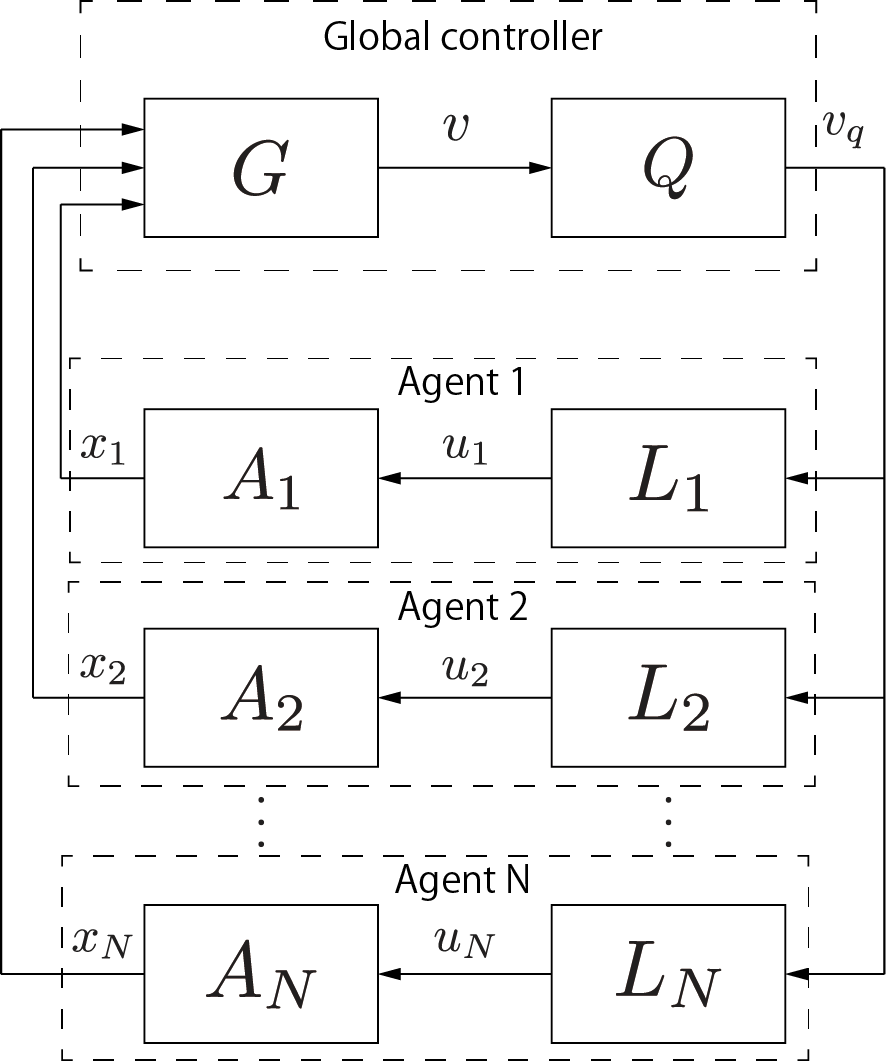 |
| 図1: Multi agent model with quantizer |
ブロードキャスト制御における量子化の必要性
ブロードキャスト制御において,全体制御器から各エージェントに対して通信路を通して制御入力を行うことが考えられる.このとき,通信路容量の制限を仮定すると,制御入力を量子化によりデータ圧縮する必要が生じる.一般的にシステムの制御入力を量子化した場合,制御対象の収束性能などに悪影響を与えることが知られている.しかし,全体制御器から制限のある通信路を介した制御入力を行う仮定を置き,制御入力の量子化を行った場合についても制御目標を達成する制御器の設計の研究は未だ行われていない.
制御入力を量子化した場合の制御手法については様々な結果が存在する[6].Brockettら[7]は,線形システムに対して量子化したフィードバック入力を用い,制御系を漸近安定とする動的な量子化器の設計を行っている.Fuら[8]は,対数型量子化器を用いた量子化において,原点の周りに不感帯を設定した場合において,量子化レベルを動的に変更することで制御量が漸近安定を満たすことを示している.Ishiiら[9]は,対数型量子化器を用いた量子化信号により,線形システムの同定を行っている.Eliaら[10]は,対数型量子化器を用いて量子化した線形システムのフィードバック入力がシステムを安定とする量子化器の最大の粗さについて述べている.このように多くの文献において,量子化制御における対数型量子化器の有用性が示されている.
研究内容
対数型量子化器の利用
本研究では,Azumaらの手法[2]に注目し,中央制御器からの出力値を理想的な対数型量子化器により量子化した場合,制御目標を達成するための手法の改善を考える.本研究では,量子化器として対数型量子化器を用いる.対数型量子化器は.量子化する値が0に近いほど量子化のステップが細かく,かつ量子化誤差が小さくなる特徴を持つ.
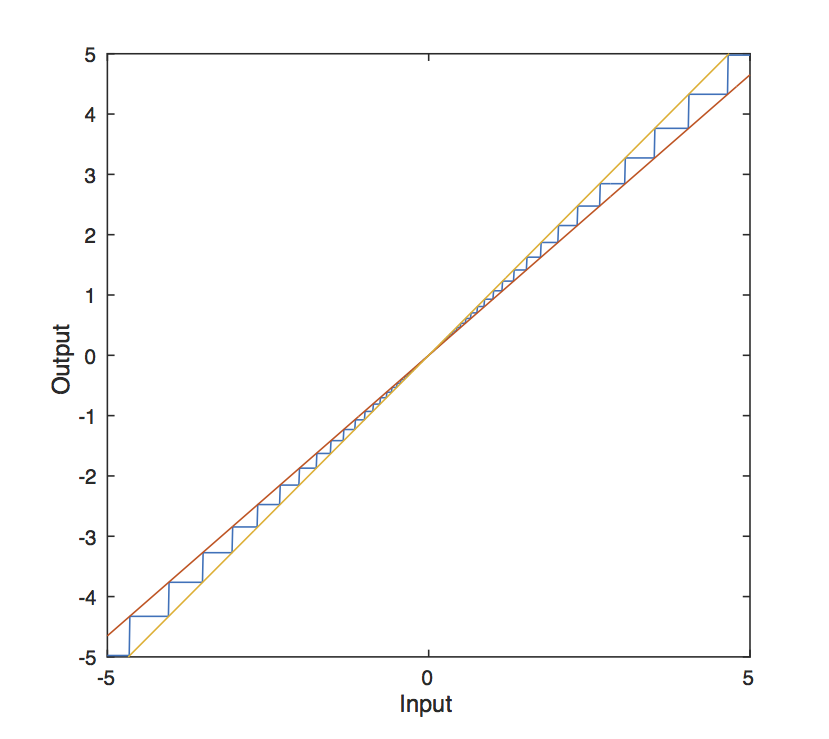 |
| 図2: Logarithmic quantizer |
制御器設計と数値シミュレーション
対数型量子化器を用いたブロードキャスト制御器設計について考える.Azumaらの先行研究[2]では,中央制御器の出力を制御目標を表す目的関数としている.先行研究では目的関数の時間的変化をローカル制御器で計算するが,本研究では,全体制御器で目的関数の変化を計算し,その変化を量子化することを考える.この改善により,通信量に制限がある場合において,制御目標を表す目的関数の最小値への収束を満たす制御器を設計することができる.
提案した制御器を利用した場合のマルチエージェントシステムの状態の収束と目的関数を示す.
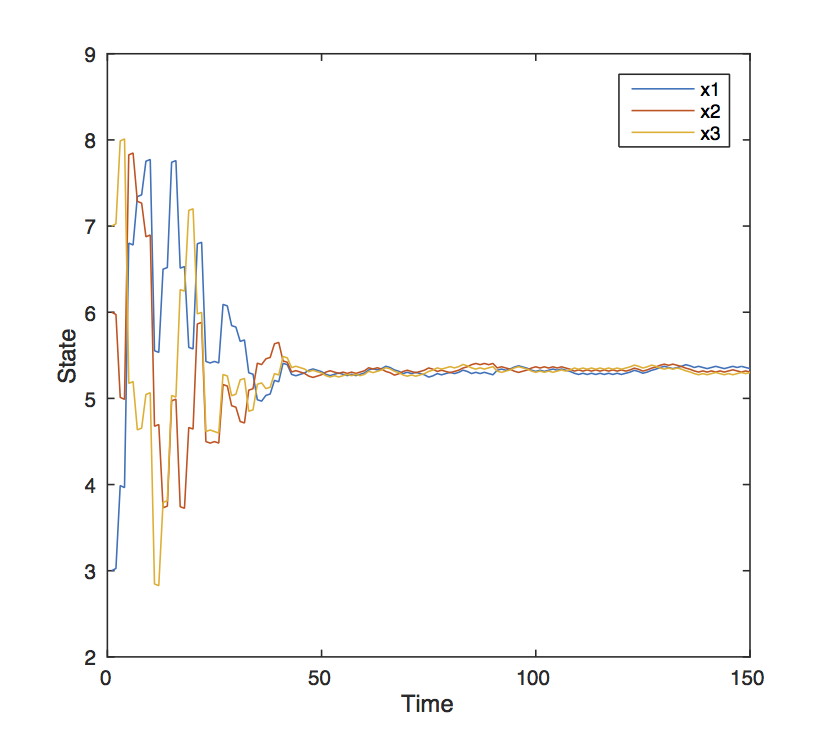 |
| 図3: State trajectories |
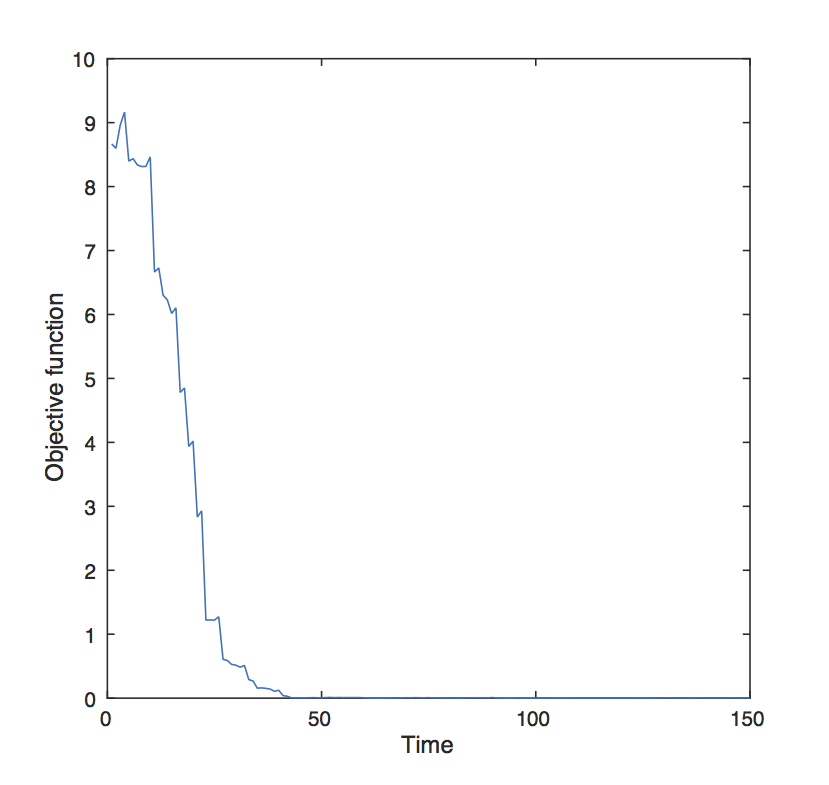 |
| 図4: Value of the objective function |
今後の課題
仮定として量子化レベルを無限小であるとおいたが,実際に実装することは不可能である.ゆえに,今後の展望としては,量子化器の0近傍に不感帯を設定し,現実の実装に近づけた仮定における議論を行う必要がある.
参考文献
[1] H.G.Tanner, "On the controlability of nearest neighbor interconnections," Decision and Control Conference, 2004, pp. 2467 - 2472, 2004.
[2] S.Azuma,R.Yoshimura,and T.Sugie, "Broadcast control of multi-agent systems," Decision and Control and European Control Conference,2011, pp. 3590 - 3595, 2011.
[3] S.Azuma,Y.Tanaka,and T.Sugie, "Multi-agent consensus under communication-broadcast mixed environment," Decision and Control Conference,2012, pp. 94 - 99, 2012.
[4] K.Das and D.Ghose, "Positional consensus in multi-agent systems using a broadcast control mechanism," American Control Conference,2009, pp. 5731 - 5736, 2009.
[5] J.C.Spall, "Multivariate stochastic approximation using a simultaneous perturbation gradient approximation," IEEE Transactions on Automatic Control,1992, pp. 332 - 341, 1992.
[6] Y.Tsumura, H.Ishii, "量子化信号を含む制御系の安定化・システム同定," 計測と制御 第44巻 第1号, pp. 70 - 77, 2005.
[7] R.W.Brockett and D.Liberzon, "Quantized feedback stabilization of linear systems," IEEE Transactions on Automatic Control,2000, pp. 1279 - 1289, 2000.
[8] M.Fu and L.Xie, "Finite-level quantized feedback control for linear systems," Decision and Control Conference, 2006, pp. 1117 - 1122, 2006.
[9] H.Ishii and T.Basar, "An analysis on quantization effects in H∞ parameter identification," Intemational Conference on Control Applications,2004, pp. 2 - 4, 2004.
[10] N.Elia and S.K.Mitter, "Stabilization of linear systems with limited information," IEEE Transactions on Automatic Control,2001, pp. 1384 - 1400, 2001.