人工衛星は，通信衛星や観測衛星として重要な存在である一方で，その生産コストは非常に大きい．そのため，人工衛星の運用年数を長期化させることが重要となるが，宇宙空間では燃料の補給ができないため，積載した燃料の量によって人工衛星の寿命が決定されてしまう問題がある．
　そこで，近年，ソーラーセイルという機構[1]が注目を集めている．ソーラーセイルとは，宇宙空間においてヨットの帆のように薄膜鏡を拡げて太陽光を受け，光子の衝突エネルギーによって推進力を得る機構である．(しばしば，ソーラーセイルを実装した人工衛星そのものがソーラーセイルと呼ばれるため，本稿においてもこの慣例に従う．)また，太陽から放射された光が物体に当たることによって発生する圧力は，太陽輻射圧と呼ばれる．ソーラーセイルの発想自体は，２０世紀中期の時点であったが[2]，ソーラーセイルの帆となる「丈夫で薄い素材」が存在しなかったため，長らく実用化には至っていなかった．しかし，近年の炭素繊維技術の目覚ましい発展によって，ソーラーセイルは実現性を帯びてきており，2010年にはJAXAが実証実験に成功している[3]．
　ソーラーセイルの主な先行研究には，ソーラーセイルを剛体とみなして姿勢の制御を行う研究[4-7]や，ソーラーセイルを質点とみなして軌道を設計・制御する研究があった．姿勢制御については，本稿では扱わないので，ここでは割愛する．
　先述したように，人工衛星の運用に際して，その運用期間を長期化していくことが重要となり，この目的のために最も重要となるのは，人工衛星の軌道である．すなわち，燃料を使用することなくミッションを達成できる軌道をあらかじめ計算しておくことが重要となる．しかし，一概に「ミッション」と言っても，多様なミッションが考えられ，そのミッション毎に適切な軌道というのは異なったものになる．たとえば，ソーラーセイルの軌道設計に関して，地球の極を観察するPole Sitterミッション[8-10]特定の軌道から特定の軌道に移動するミッション[11-13]考えられてきた．本研究においては，同一の領域に，燃料を消費することなく長期に渡って留まる必要のあるミッションを対象とする．例として，先述したPole Sitterミッション，太陽の観測ミッション，宇宙風の試料採取ミッションなどが挙げられる．この目的をもって軌道を設計するにあたり，モデルは大別して次のものがある：

• １つの天体の重力下においてソーラーセイルの振る舞いの解析を行うモデル．すなわち，太陽輻射圧を考慮した二体問題である．一般的な二体問題と比較し，「ソーラーセイルの重力が天体に影響を及ばさない」仮定をおいている．
• ２つの天体の重力下においてソーラーセイルの振る舞いの解析を行うモデル．すなわち，太陽輻射圧を考慮した三体問題である．本研究では，三体問題に次の近似を与えた問題を考える：
  • １つの天体が，もう１つの天体の周りを円軌道で公転している．
  • ソーラーセイルの重力が天体に影響を与えない．
  このような三体問題は，とくに円制限三体問題（Circular Restricted Three Body Problem, CRTBP）と呼ばれる．
• ３つ以上の天体の重力下においてソーラーセイルの振る舞いの解析を行うモデル．本研究においては扱わない．

　燃料を消費することなく太陽観測等のミッションを達成できる軌道とは，すなわち，これらのモデルに埋め込まれた周期軌道[14]である．周期軌道とは，外部からの制御入力を入れずとも，一定の時間（周期）後に，同一の位置に同一の速度で帰還するような軌道を指す．たとえば，太陽を観測するミッションに際しては，太陽の周辺に留まる軌道が重要であり，この軌道として，太陽-地球-ソーラーセイルの円制限三体問題に埋め込まれた周期軌道はひとつの候補であろう．
　しかし，周期軌道の計算には困難が伴うことが多い．先述したソーラーセイルの軌道設計のモデルは，非線形ダイナミカルシステムであり，非線形性を持つダイナミカルシステムの解析は難しいためである．ただし，ここでいう「解析の難しさ」とは，周期軌道を解析解として導出することができない，という意味での難しさである．
　本研究では，従来のソーラーセイルの軌道計算手法の問題点を解消するようなあたらしい軌道計算手法を考案することを目的とする．そのために，次のような順序で研究を行った．

1. 一定の条件を満たす非線形システム（当然ながら，ソーラーセイルの軌道設計モデルはこの条件を満たす）に適用できる周期軌道計算アルゴリズムを提案する．
2. 上記のアルゴリズムを二体問題モデルに適用する．
3. 上記のアルゴリズムを三体問題モデルに適用する．

　ここで提案する新しい周期軌道計算アルゴリズムとは，Act-and-Wait遅れフィードバック制御を用いた計算アルゴリズムである．そのため，まずはAct-and-Wait遅れフィードバック制御とはどのようなものであるのかを説明し，これを用いた軌道計算手法について説明する．

　物理学，生態学など数多くの分野において，カオス現象と呼ばれる現象が発見されている[15,16]．カオス現象とは決定論的であるにも関わらず予測不可能な挙動を示す現象であり，研究者によってその定義は異なるが，一般的に，(1)初期値に対して鋭敏性を持つ(2)分割不可能性を持つ(3)不安定周期軌道が稠密に存在する，などの性質を持つ．特に，工学的な発展性などを考慮すると，カオス現象の持つ予測困難性は望ましくない性質である．したがって，外部から適切な制御入力を与えることによって，周期的な振る舞いなどに制御していくことが重要であり，この概念はカオス制御[17]と呼ばれる．本章で扱う遅れフィードバック制御（Delayed Feedback Control, DFC）とは，カオス制御のための手法としてPyragasによって考案された手法の一つである[18]．
　カオス制御をするにあたり，一般的な制御問題のように，系に潜在している周期軌道を目標軌道に設定し，その偏差にフィードバックをかけることによって状態を目標軌道に追従させることは難しい．なぜならば，カオスシステムの解析は系の非線形性のため困難であり，系に埋め込まれた周期軌道を計算すること自体できないことが多いためである．そこで，周期軌道の厳密な位置を知ることなく，周期軌道に追従させる手法として，DFCが提案された．DFCは，「安定化したい不安定周期軌道の周期」が既知であるという条件下において，現在の状態と１周期前の状態との偏差にフィードバックすることによって軌道の安定化を行う．また，DFCを拡張した拡張DFCも提案されている[19]．
　ところで，「制御入力」を与えることによって周期軌道を計算するというのはわかりにくい考え方であるため，補足をする．そもそも非線形ダイナミカルシステムにおいて周期軌道の計算が困難であるのはなぜかというと，これは周期軌道の不安定であるためである．周期軌道が不安定であるとは，周期軌道から少しでも状態がずれると，そのまま周期軌道から離れていってしまうような性質を意味する．逆に，もし周期軌道が安定であれば，数値計算において十分に時間発展させることによって，周期軌道上に状態が落ち着くため，容易に計算できるのである．DFCとは，不安定な周期軌道を安定な周期軌道に変化させる制御手法であるため，非線形ダイナミカルシステムに埋め込まれた周期軌道の計算の困難さを取り除くことができるのではないか，というのが本研究におけるキーアイデアである．
　DFCを利用するにあたり，安定化を保証するゲイン行列をいかに計算するか，という問題が非常に重要となる．一般に，遅れを含む微分方程式は解析が困難であり，経験や度重なる試行によってゲイン行列を設計することが多いが，局所的な状態の変化率から適応的にゲイン行列を決定する研究がある[20,21]．また，DFCによる安定化を考える研究において，しばしばOdd Number Limitationという安定化不可能条件に関する考察が現れる．Odd Number Limitationとは，もともとは離散時間系において発見されたDFCの安定化不可能条件であり[22]，その後，連続時間系においても，Odd Number Limitationに準ずる制約が存在することが報告されている[23,24]．
　また，Odd Number Limitationに関する定理には反例が存在することも示されており[25]，さらにその結果を踏まえて，文献[23,24]における定理に修正を行った論文も存在する[26,27]．このように，安定化不可能条件に関しては今後も多くの議論がなされていくと考えられる．
　安定化不可能条件のアプローチとは別に，不安定周期軌道の安定化可能条件に対して解析的にアプローチをできるAct-and-Wait遅れフィードバック制御（Act-and-Wait Delayed Feedback Control, AWDFC）というDFCが考案されている．
　Act-and-Wait Delayed Feedback Control(AWDFC)とは，１周期ごとに制御入力のON-OFFを切り替えるDFCである．文献[28]によってAWDFCの概念が提唱され，文献[29]において，離散システムを対象としてより深い研究がなされている．そして，文献[30]では，AWDFCの有効性を実験によって示している．また，文献[31]では，本研究で扱うAWDFCとは異なるスイッチングをした場合（スイッチングの周期と周期軌道の周期が異なっている場合）の安定化可能条件への考察をしている．
　さらに，文献[32]では，時変線形システムや非線形システムに埋め込まれた周期軌道を安定化するための解析的な条件を導出している．しかし，これらの研究においては，どのようにゲイン行列を設計すれば安定化を保証するかについては考えておらず，経験や勘にたよったゲインの設計を行なっていた．
　そこで，本研究では，AWDFCを用いることによってこの問題を解決する手法を提案している．具体的には，安定化可能条件と等価な多変数関数の最小化問題を解くことによってシステマティックにゲイン行列を設計できることを示している．また，先行研究では定数ゲイン行列しか扱っていなかったが，この手法を用いることによって自由度の高い時変ゲイン行列を設計できる．論文では，自由度の高いゲイン行列の例をいくつか提示し，閉ループ系の状態の解析解の導出や，シミュレーションによる二次元の非線形システムの安定化を行なっている．

　AWDFCによる未知の周期軌道の計算アルゴリズムを使うにあたり次の仮定をする：

• 非線形ダイナミカルシステムがパラメータpによって一意に定まる無限個の周期軌道を持っており，また，パラメータの変動にしたがって，埋め込まれた周期軌道も連続的に変動すること
• あるパラメータpにおける周期軌道の位置が数値計算などによってわかっていること
• パラメータpに対応する周期軌道を安定化するゲイン行列を知っていること（これは先述したシステマティックなゲイン行列の設計手法によって設計できる）

このとき，非線形システムのパラメータに十分に小さな摂動を与えても，同一のゲイン行列によって系に潜在する周期軌道を安定化できることを証明した．
　したがって，次の手順に従って，未知の周期軌道を知ることができる：

1. パラメータpに対応する周期軌道が既知であるので，これを安定化するゲイン行列を計算する
2. パラメータpに小さな摂動を加えた非線形システムに埋め込まれた周期軌道を，ステップ１において計算したゲイン行列を用いて安定化し，数値計算上で十分に時間発展させることでこの周期軌道に収束させる．
3. 摂動を与えたパラメータを，パラメータpとみなし，ステップ１に戻る．この操作を，所望のパラメータp1に到達するまでくりかえす．

　このアルゴルズムを，AWDFC-Chasing Periodic Orbits Methodと呼ぶこととする．論文では，この手法を用いて，パラメータを持つ低次元非線形ダイナミカルシステムの未知の周期軌道を計算する例を提示している．

　ソーラーセイルの，太陽光によって推進力を得る性質から，「影響を考慮する天体が恒星であるのか否か」によってそのモデルを大別できる．ソーラーセイルの軌道設計の観点からは，いずれの場合においても，系に埋め込まれている周期軌道の扱いには大きな違いがないため，本研究では特に「太陽とソーラーセイル」の二体問題モデルのみを考えている．
　太陽輻射圧を考慮しない二体問題に関しては，その軌道が完全に解析できる[33]．このとき，二体問題に埋め込まれた周期軌道は，軌道面に星体が含まれており，Keplerian Orbitと呼ばれる．　一方で，太陽輻射圧を考慮した二体問題においては，太陽輻射圧の影響によってKeplerian Orbitがずれ，軌道面に天体が含まれていないNon-Keplerian Orbitとなる．この軌道はDisplaced Periodic Orbit (DPO)と呼ばれる円軌道であり，安定性や可制御性などについても多くの研究がなされている[34-37]．また，DPOを目標軌道としたときに，Lightness Parameterやソーラーセイルの姿勢角を制御入力として用いることによって，目標軌道に追従させる研究[38]や，Solar Electric Propulsionという別の推進力を兼ね備えたハイブリッドソーラーセイルをDPOに配置する研究[9]などがあった．
　DPOの一つをAWDFCによって安定化した結果を示す．

図1: 太陽輻射圧を考慮する二体問題モデルにおけるソーラーセイルの振る舞いを図示している．図(a)は，AWDFC入力を入れなかった場合の軌道であり，図(b)はAWDFC入力を入れた場合の軌道である．明らかに図(a)では周期軌道が不安定となっていて，図(b)では安定となっている

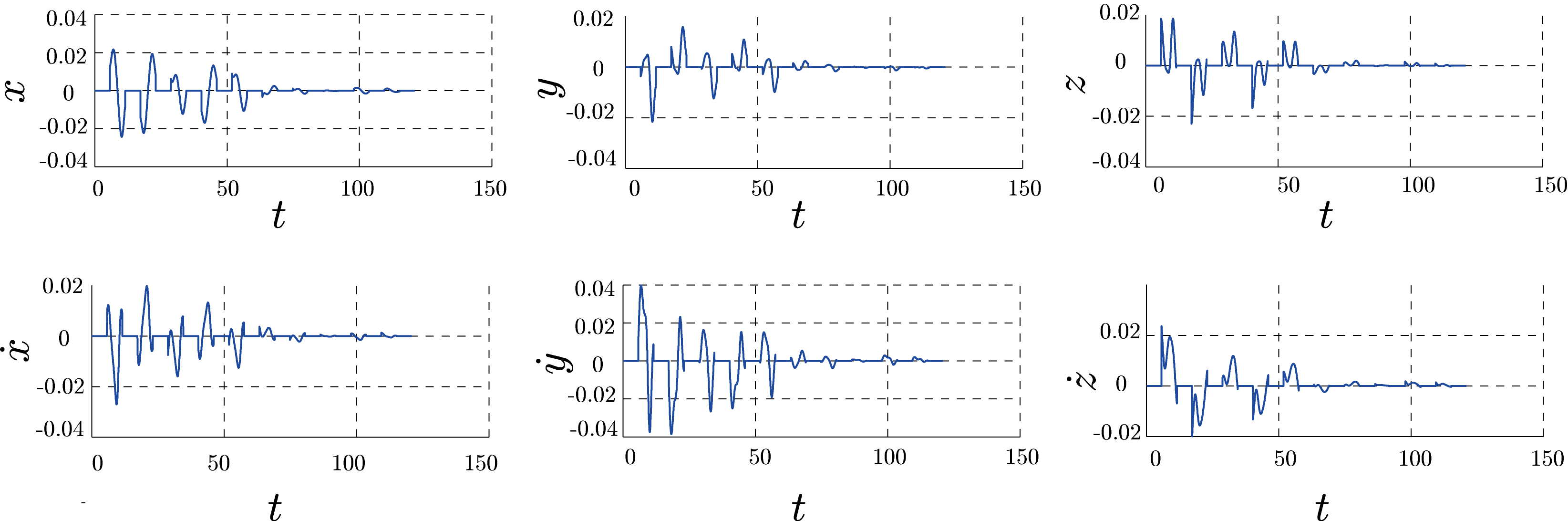
図2: 太陽輻射圧を考慮する二体問題に埋め込まれた周期軌道を安定化するAWDFC入力．時間発展にしたがって入力が零に収束していることに注意されたい．これは，ソーラーセイルが周期軌道に完全に乗っていることを示している．

　太陽輻射圧を考慮するCRTBPは，考慮しないCRTBPよりも太陽輻射圧を考慮するだけ高度であり，難しい問題である．しかし，太陽輻射圧を考慮しないCRTBPにおける手法はそのまま太陽輻射圧を考慮するCRTBPにも使用することができるため，まずは太陽輻射圧を考慮しないCRTBPについて説明する．

　CRTBPは強い非線形性を持ち，本研究で興味の対象となっている周期軌道の位置を解析解の形で得ることはできない．そこで，周期軌道の位置を知るために使われる方法は，系の平衡点（CRTBPにおける平衡点は特にLagrange点と呼ばれる）のまわりで線形近似したシステム，あるいは高次近似したシステムを計算し，この近似システムに埋め込まれた周期軌道を計算する方法である[39-41]．平衡点に十分近い領域ならば，平衡点のまわりで線形近似したシステムの固有値を求め，固有値に純虚数固有値が含まれていれば，この固有空間に周期軌道が存在する．しかし，CRTBPは強い非線形性を持つため，平衡点から離れれば離れるほどその近似性能は下がり，平衡点から離れた領域の正確な周期軌道を知ることは難しくなる．そこで，近似システムの解を初期条件として数値計算することで正確な周期軌道が求められている[41,42]．
　また，あるパラメータに対応する周期軌道が既知であるときに，この軌道を初期条件として利用して，パラメータを徐々に変化させながら周期軌道を補足していくPseudo Arclength手法と呼ばれる方法がある．CRTBPに埋め込まれた周期軌道は，軌道の振幅や周期などをパラメータとして持っているため，先述した方法であらかじめ求めておいた周期軌道を利用することによって，これらの周期軌道を求めることができる[43]．文献[43]では，周期軌道に関する分岐図を調べており，CRTBPに埋め込まれた周期軌道の族が網羅的に述べられている．
　Pseudo Arclength Methodは，パラメータを徐々に変化させながら周期軌道を計算していく点においてAWDFC-Chasing Periodic Orbits Methodに似ているが，Pseudo Arclength Methodには計算の収束に理論的な裏付けが存在しない．より詳しい情報については，次の文献などを参考にしてほしい[44-46]．

　太陽輻射圧を考慮したCRTBPにおいても，ソーラーセイルの姿勢角が特殊な条件を満たしている場合には，太陽輻射圧を考慮しないCRTBPに対する手法と同様の方法によって周期軌道を概算できる[47]．すなわち，平衡点のまわりの近似システムに対して解析解を求め，数値計算で精度を上げればよい．しかし，姿勢角がその条件を満たしていないとき，近似システムに周期解が存在せず，したがって従来の手法を適用できない．
　そこで，本研究においての最終的な目標は，「姿勢角が特殊な条件を満たしているときの周期軌道を計算し，これを初期条件として利用し，AWDFC-Chasing Periodic Orbits Methodによって周期軌道を計算していくこと」である．この目標を達成するにあたり，必ず考えなければならないことは，CRTBPに埋め込まれた周期軌道はAWDFCで安定化できるのかという点である．この問題を考えるにあたり，DFCによって太陽輻射圧を考慮しないCRTBPの周期軌道を安定化している研究[48]や，太陽輻射圧を考慮するCRTBPに埋め込まれた周期軌道を安定化する研究[49,50]が参考になる．しかしながら，これらの論文では，DFCにおいて最も重要となるゲイン行列の決め方について，理論的な検証やアルゴリズムなどが与えられていない問題が存在している．そのため，システマティックにゲイン行列を設計できるAWDFCを用いることによって太陽輻射圧を考慮するCRTBPに埋め込まれた周期軌道の安定化を行う．
　ところで，本研究では，決められた領域に制御入力なくとどまり続けることのできる軌道を設計したい，という目標を達成するにあたり，Lightness numberや姿勢角が既知の定数パラメータであるという仮定をおいている．しかし，これとは逆に，目標軌道が既知で，Lightness numberや姿勢角などを制御入力として用いることによって，目標軌道に収束させるアプローチも存在する．たとえば，文献[51,52]では，非線形項の影響を太陽輻射圧による推進力によって打ち消すように，Lightness numberと姿勢角を変化させて目標軌道への収束を達成していた．あるいは，文献[53,54]では，Solar Electric Propulsionのような別の推進力を実装されているハイブリッドソーラーセイルについて，非線形項を打ち消すように推進力を利用することによって，二体問題モデルにおけるDPOを創出し，これを安定化していた．他にも，円制限三体問題を近似したシステムであるHill's equationに対して最適制御の手法を適用し，Lightness numberと姿勢角による制御を行なっている研究もあった[55]．
　本研究において，パラメータを固定して周期軌道を計算する方法を選んだのは，Lightness numberや姿勢角を制御入力として用いることが実用上困難であると考えたためである．なぜならば，たとえば姿勢角を変化させるためには，姿勢制御用のスラスターを使うために燃料を消費しなければならないし，Lightness numberを変化させるためには，人工衛星のスピンの角速度を上げるなどして帆の面積を増やさなければならず，このとき燃料を消費してしまうためである．
　そのため，本研究においては，回転座標系においては，Lightness numberや姿勢角が一定である仮定をおき，このときの周期軌道を安定化することを考えている．

　先述したように，太陽輻射圧を考慮するCRTBPにおいては，人工衛星の姿勢が特殊な条件を満たせば，平衡点のまわりに周期軌道が存在する．太陽輻射圧を考慮するCRTBPにおける平衡点は，円制限三体問題におけるLagrange点に相当していることから，しばしば人工Lagrange点(Artificial Lagrange Points)と呼ばれる．太陽輻射圧を考慮する円制限三体問題においては，系のパラメータとしてLightness numberや姿勢角が存在する．先行研究では，これらのパラメータによって，平衡点の位置が変化し，連続体(continuum)として存在することが示されている[56]．また，本研究においては，ソーラーセイルの帆の表面で光が乱反射せず，完全反射することを仮定しているが，光が乱反射する場合に人工Lagrange点の連続体がどのようになるかも調べられている[57]．他にも，楕円制限三体問題に埋め込まれた平衡点についても論じられている[58]．
　太陽輻射圧を考慮するCRTBPにおいて，人工Lagrange点において線形化したシステムが純虚数固有値の組みを一組または二組もっていることがわかっている[47]．純虚数固有値の組みを二組もっているケースにおいて，それぞれの組みの固有値に対応する周期軌道が存在し，また，それぞれに対応する固有空間は直交している．これらの周期軌道に関して，より公転面の近くに存在する周期軌道をPlanar Lyapunov family，そうでない周期軌道をVertical Lyapunov familyと呼ぶ[59,60]．これはCRTBPにおける呼び方に対応している．また，太陽輻射圧を考慮しないCRTBPにおけるHalo軌道の議論のように，Lindstedt-Poincáre手法を用いて，高次の近似解を調べている研究もあった[58,61]．
　本研究においては，Planar Lyapunov Familyの周期軌道の安定化を行った．ここで，太陽と地球間の距離を１とおき，地球と共に公転する回転座標系において解析を行なう．今回安定化を行った周期軌道の図を以下に示す．

図3: 太陽輻射圧を考慮する三体問題モデルにおけるソーラーセイルの振る舞いを図示している．図(a)は，今回安定化を行ったPlanar Lyapunov Familyの周期軌道であり，図(b)は入力を入れなかった場合のソーラーセイルの振る舞いである．明らかに不安定な振る舞いをしていることがわかる．

　次に，AWDFCによって安定化を行った図を示す．ただし，先行研究によって，次の条件が等価であることがわかっている：

• ゲイン行列Kによって，非線形システムに埋め込まれた周期軌道が安定化されること．
• 非線形システムに埋め込まれた周期軌道の周りで線形化を行うことによって，時変線形システムを生成する．このとき，ゲイン行列Kによって，時変線形システムに埋め込まれた周期軌道が安定化されること．

　下図では，時変線形システムに埋め込まれた周期軌道を安定化している．

図4: AWDFC入力を与えた線形化システムの閉ループ系の振る舞い

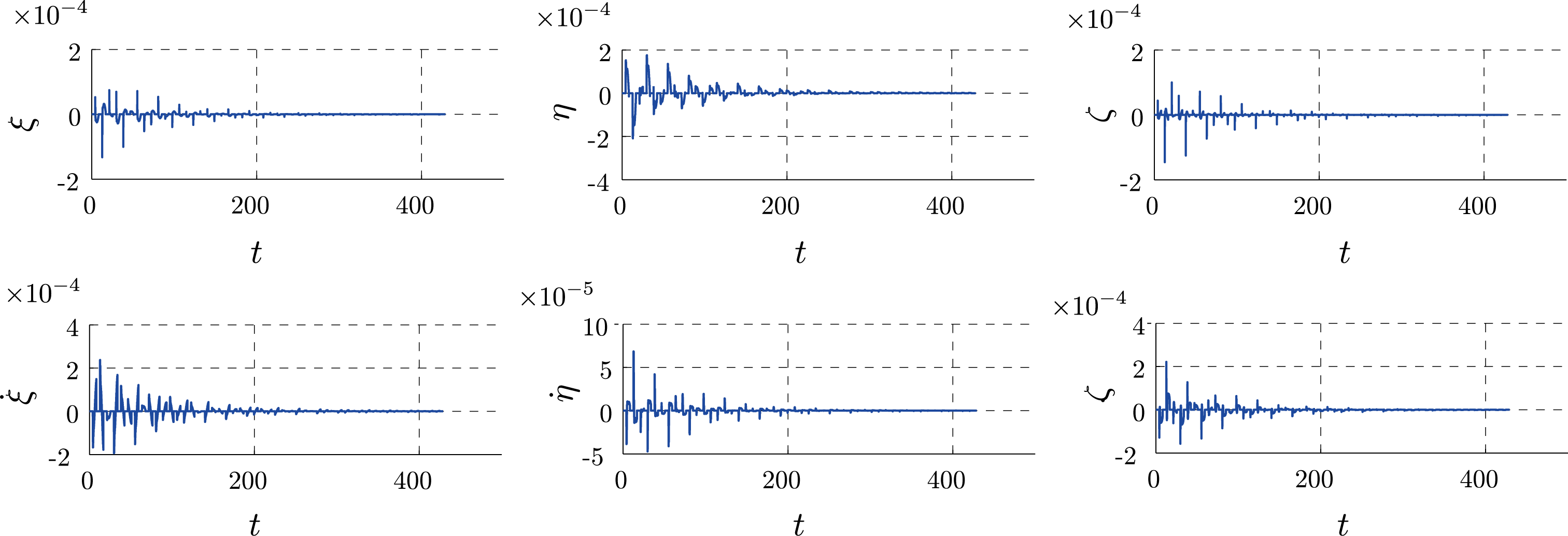
図5: 線形化システムの閉ループ系に印加しているAWDFC入力

　一般的な非線形ダイナミカルシステムに適用可能であるAWDFCのゲイン行列の設計手法を提案した．また，これまでは「既知の周期軌道を安定化」するだけであったが，AWDFCを用いることによって全く未知の周期軌道を計算できることを示した．実際に，この手法を低次元の非線形ダイナミカルシステムに用いて妥当性を確かめた．
　次に，高次元（６次元）の非線形ダイナミカルシステムである二体問題モデル，三体問題モデルに埋め込まれた周期軌道を安定化するようなAWDFCのゲイン行列を計算し，実際に安定化を行った．

　円制限三体モデルは非常に不安定性が強く，不安定周期軌道を安定化することが可能であっても，収束領域（Basin of Attraction）が非常に狭くなってしまう問題があった．そのため，Basin of Attractionをより広く取ることができるようなゲイン行列がどのような行列であるのかを調べていきたい．また，現段階では，AWDFC-Chasing Periodic Orbits Methodをソーラーセイルのモデルに用いることはできていない．理由としては，理論的には可能であるが，ソーラーセイルのモデルのような高次元システムではゲイン行列の計算コストが非常に大きく，何度もゲイン行列を計算し直すAWDFC-Chasing Periodic Orbits Methodが実用的ではないことが挙げられる．そのため，ゲイン行列の計算コストを下げるための方法を考えていきたい．