研究背景と先行研究
洋上風力発電
近年,化石燃料の大量消費による環境汚染が問題視され,原子力発電の危険性が問われている.そこで,自然エネルギー由来の再生可能エネルギーが注目を浴びており,再生可能エネルギーのひとつとして風力がある. 風力は古くから製粉や灌漑などに利用されてきており,19世紀後半には発電機としての風力の利用が始まった.そして,技術の発展に伴い,発電機は大型化し,洋上風力発電をはじめとする新たな方式が考案されている[1].洋上風力発電は,風力発電機を洋上に設置する試みであり,洋上では,広大な設置可能領域があることや,陸上に比べて安定して強い風が吹いていることなどから,大きな発電量が期待できるというメリットがある[2].
洋上風力発電の設置方式には着床式と浮体式がある[3].着床式とは,海底から海面まで基礎構造物を建設し,その上に風車を設置する方式である.浮体式とは,基礎構造物を海底に係留し海面に浮かべ,その上に風車を設置する方式である.設置方式の違いから,着床式は浅い海域に設置するのに適しており,欧州をはじめとしていくつかの大規模なウィンドファームが着床式により設置されている.また,日本の近海のように深い海域では着床式の建設は困難となるため,浮体式での設置となる.浮体式の主要な設置形式のひとつにSpar型と呼ばれるものがあり,その模式図を示す.
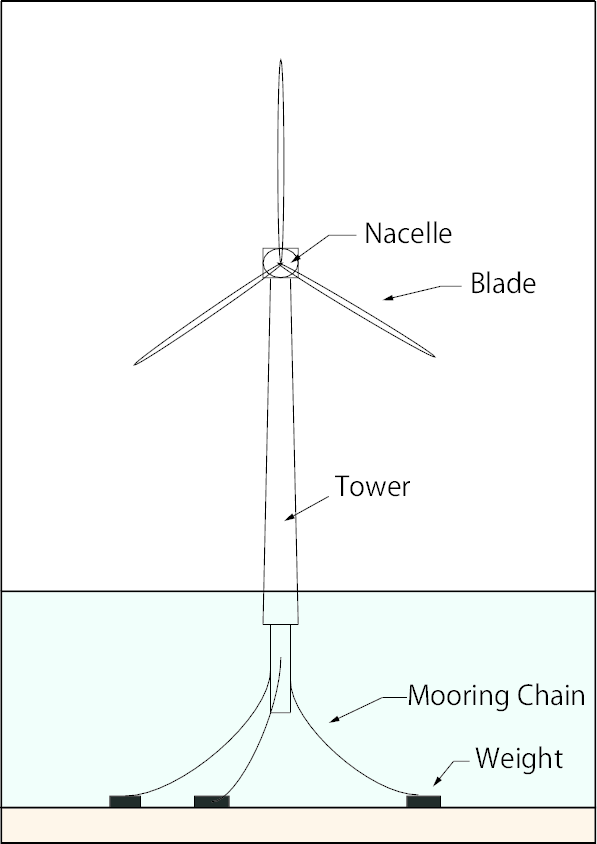 |
| 図1: Spar Type Floating Wind Turbine |
洋上風力発電の動揺問題
浮体式の建設にはいくつかの課題が残されている.たとえば,浮体式では,海面に浮かんだ風車と基礎構造物は,風や波の影響によって生じる負荷を受けて動揺する.この動揺によって,ブレードが傾くことにより発電効率は低下し,発電システムに繰り返し負荷がかかることにより耐久性を損われるなどの問題が生じる.したがって,浮体式洋上風力発電が安定した発電方式として確立するためには,浮体の動揺抑制は重要である.
解析にあたり、風や波のモデル化が必須である.[4]では,風による負荷のモデルが提示されている.[5][6]では,波による負荷がモリソン式などから見積もられ,動揺解析がされている.
風力発電における制御方式のひとつにブレードピッチ角制御がある.ブレードピッチ角制御はブレードのピッチ角を変えることで,発電出力や風による負荷の大きさを調節する方式である.ブレードピッチ角制御に関する研究では[7][8]が挙げられる.さらに,それぞれのブレードのピッチ角を別々に制御する個別ブレードピッチ角制御に関する研究では,[9][10]が挙げられる.また,風速一定,波による影響がないという条件化において,[11]では,発電出力,浮体の動揺,浮体のギアに生じるジャイロモーメントの抑制の制御について考察されている.
研究内容
Spar型洋上浮力発電システムのモデリング
本研究では,Spar型浮体式洋上浮力発電システムを2次元回転モデルとして捉え,ブレードと正対する方向の運動を解析する.ブレードに作用する風による負荷,タワー海底部分に作用する波による負荷,変位に対する復元力によって トルクが生じ,浮体の運動が定まる.
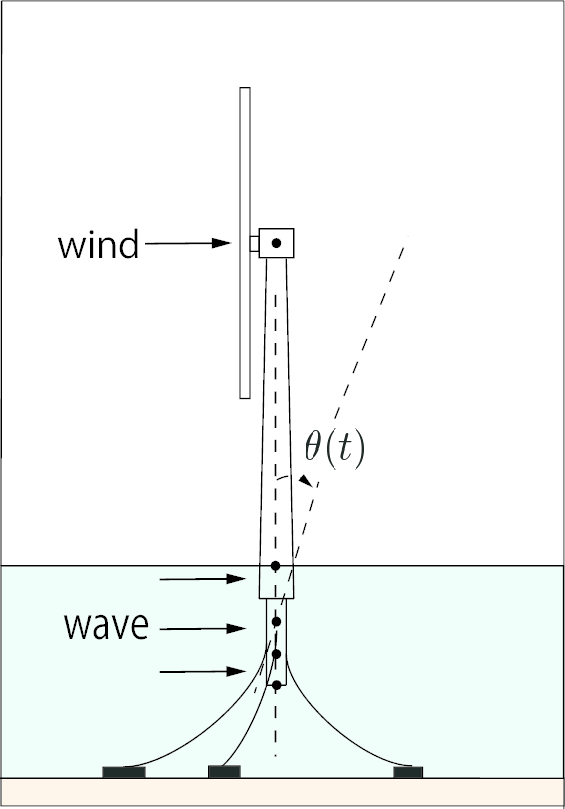 |
| 図2: The Rotating Model to Analize |
本研究では、風速の変動に着目する.本来,風速は不規則に高い周波数で変動しており,この特徴を陽に考慮した研究は少ない.風速の変化を正確に観測し,その情報をブレードピッチ角に反映させることは,現実的ではない.これは,風速の変化を正確に観測するセンサがないことや,風速の変化に伴ってブレードピッチ角を細かく変動させるアクチュエータがないことに由来する.したがって,風速が変化することにより,平均風速(観測風速)と変動風速(実際に吹いている風速)との間に誤差が生じ,これを観測で生じる不確かさと捉える.風速の不確かさを許容する制御系を二次安定化理論に基づいて設計する.
制御系設計と数値シミュレーション
二次安定化理論にもとづいて制御系を設計する.二次安定化理論は,不確かさを有する線形時変システムの安定性を解析する手法のひとつである.Riccati方程式の正定解を用いて制御則を構成,システムの有する平衡点の大域的一様指数安定性が保証される[12].
回転モデルに二次安定化理論に基づいて設計した入力を印加したときの浮体の動揺と入力(3つのブレードピッチ角の和)を示す.
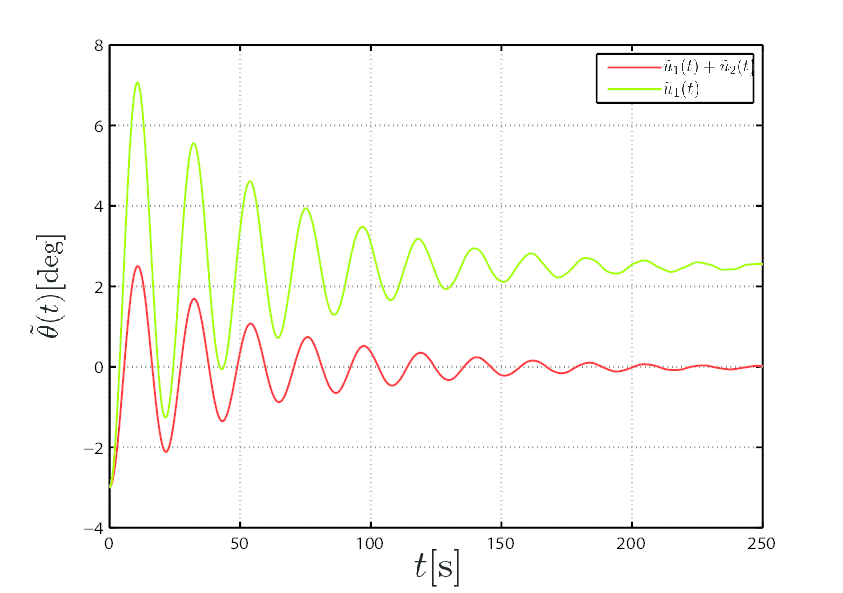 |
| 図3: Time Response of Phi |
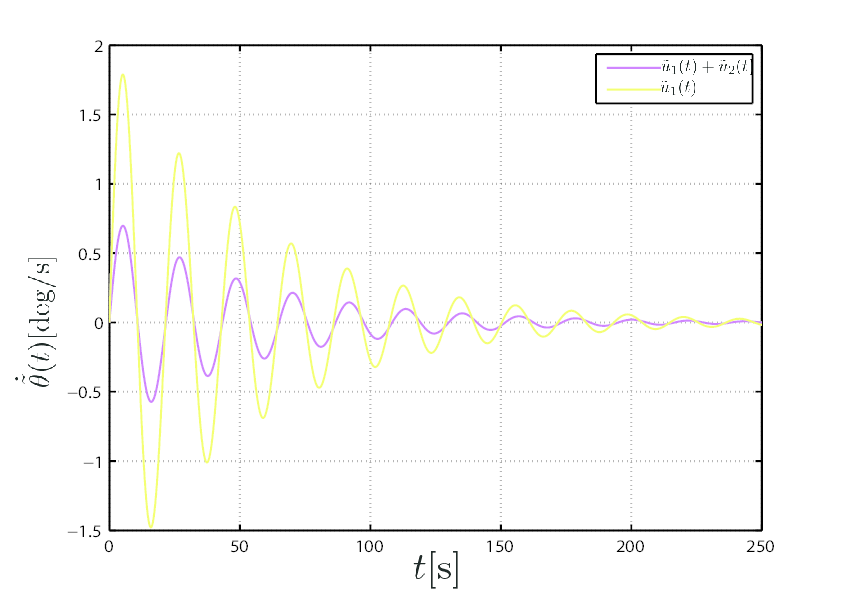 |
| 図4: Time Response of Time Derivative of Phi |
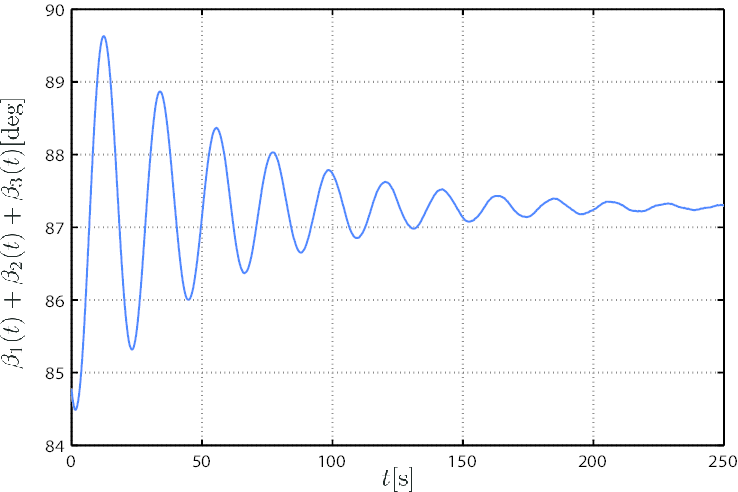 |
| 図5: Time Response of Input(The Sum of Three Blade Pitch Angles) |
今後の目標
波のモデリング
風速に関しては変動を考慮しているが,波に関しては一定流速をもつ流れとしてモデル化をしている.したがって,波の特徴をより反映したモデルをもちいて制御系を設計する.
洋上風力発電を取り巻く包括的な制御系の設計
本研究では,浮体の動揺抑制に着目したが,洋上風力発電を取り巻く制御問題は複数ある.したがって,それらを考慮した包括的な制御系の設計が必要である.
参考文献
[1] 牛山泉, "風車工学入門," 森北出版株式会社, 2002.
[2] S. Butterfield, W. Musial, J. Jonkman, and P. Sclavonous, Engineering challenges for floating offshore wind turbines, Copenhagen.Denmark,Octover 26-28, 2005.
[3] L. Pao and K. Jonson, "A tutorial on the dynamics and control of wind turbines and wind farms," in Proceedings of American Control Conferences, vol. June, pp. 2076-2089, 2009.
[4] A. Pintea, H. Wang, N. Christov, P. Borne, and D. Popescu, "Modeling and power regulation of horizontal variable speed wind turbines," Studies in Infomatics and Control, pp. 305-312, 2011.
[5] M. Karimirad, Q. sc.essonnier, Z. Gao, and T. Moan, "Hydroelastic code-to-code comparison for a tension leg spar-type floating wind turbine," Marine Structures, vol. 6, no. 4, pp. 412-435, 2011.
[6] Y. Lee, C. Ho, and Z. Huang, "Hydrodynamix responses of a spar-type floating wind turbine in high waves," Journal of Mechanics, pp. 1-8,10, 2014.
[7] F. Inthamousson, D. Bianchi, H. Battista, and J. Mantz, "Lpv wind turbine control with anti-windup features covering the complete wind speed range," IEEE Transactions on Energy Conversion, vol. 29, no. 1, pp. 259-266, 2014.
[8] Z. Mu, L. Jizhen, and L. Zhongwei, "Mixed h2/h pitch control of wind turbine generator system based on exact linearization and regional pole placement," in Proceedings of Control Conference, pp. 6982-6986, 2014.
[9] V. Petrovic, M. Baotic, and N. Peric, "Reduction of wind turbine tower oscillations based on individual pitch control," in Mediterranean Conference on Control Automation, pp. 1499-1505, 2012.
[10] H. Namik and K. Stol, "Individual blade pitch control of a spar-buoy floating wind turbine," IEEE Transactions on Control Systems Technology, vol. 22, no. 1, pp. 214-223, 2014.
[11] 青田諒, ジャイロモーメントを考慮した浮体式洋上風力発電モデルの解析, 東京工業大学修士論文, 2012.
[12] I. R. Petersen and C. V. Hollot, "A ricatti equation approach to the stabilization of uncertain linear systems," Automatica, vol. 22, no. 4, pp. 397-411, 1986.