研究背景・先行研究
非協力ゲーム理論
近年複数のエージェント同士が影響を及ぼしあうマルチエージェントシステムの応用が盛んである. マルチエージェントシステムの一つに, 非協力ゲーム理論[1]を用いたシステムが存在する. 非協力ゲーム理論では, エージェント同士がお互いに協力せずにふるまう. 各エージェントは効用関数という状態の関数の値をより大きくしようと状態を変化させる. 非協力ゲームは静的で状態が離散的なものが扱われることが多いが、エージェントの振る舞いを確認するためには, 動的な非協力ゲームを扱う必要がある.
ナッシュ均衡
非協力ゲームにおいて, ナッシュ均衡と呼ばれる状態になるのが望ましい. ナッシュ均衡とは, すべてのエージェントがその状態から状態を変化させようとしない状態のことである. ナッシュ均衡には安定なものと不安定なものが存在する. 不安定なナッシュ均衡を安定化させるため, 非協力ゲームをシステムとして扱った解析が行われてきた.
疑似勾配ゲーム
非協力ゲームをシステムとして扱う手法のひとつに疑似勾配(pseudogradient)ゲームがある. 擬似勾配ゲームにより, 効用関数の値が大きくなる方に自分の状態を変化させるというエージェントの振る舞いを表すことができる. 疑似勾配ゲームでは, 各エージェントの状態の微分が, そのエージェントの効用関数をそのエージェントの状態で偏微分したものに, 実数定数をかけたものとなる[2][3][4]. この定数のことを感度という. [2]では感度は既知として扱っているが, 感度はエージェント個人に関わるパラメータであり, 未知となる場合がある.
税-補助金アプローチ
不安定なナッシュ均衡を安定化させる手法として, 税-補助金アプローチが存在する. 税-補助金アプローチでは, 税を徴収しその状態での効用関数の値を小さくする, もしくは補助金を与えその状態での効用関数の値を大きくするといった手法で, エージェントにより好ましいふるまいをさせるものである[5][6][7]. 税と補助金はインセンティブとよばれる. インセンティブは状態の関数になる. システムの設計者が余計なコストを支払わずに不安定なナッシュ均衡の安定化を行うためには, インセンティブの合計が0となる必要がある. [8]において, インセンティブの総和が0になる関数が用いられている. [8]では, 擬似勾配ゲームにおける感度が未知の場合に対して, インセンティブの関数のパラメータを決定し非協力ゲームのシステムにおいて不安定なナッシュ均衡の安定化を行なっている. 本研究では, 擬似勾配ゲームにおける感度が未知の場合に対して, インセンティブの関数のパラメータを決定せず, 動的なものとして扱い安定化を行なう.
研究目的
本研究では, システムに未知の部分が含まれている場合の動的な非協力ゲームでの不安定なナッシュ均衡の安定化を行う. 税-補助金アプローチを用いてナッシュ均衡の安定化を行うため, インセンティブの設計を行う. インセンティブの合計が0になるような設計を行う.
問題設定
本研究では, Nエージェントの非協力ゲームを扱う. この非協力ゲームは動的で, 状態が連続であるとする. 各エージェントの効用関数は状態に対して二次形式のもののみを扱う. 効用関数に関するすべてのパラメータは既知のものとする. 効用関数に関するすべてのパラメータが既知のため, ナッシュ均衡も既知となる. この効用関数から疑似勾配ゲームを用いてシステムを導出する. 疑似勾配ゲームを用いる際に, 未知の定数である感度がかかわるため, システムは未知となる. システムが未知のため, モデルが未知であっても制御が可能である適応制御を用いて制御を行う.
主結果
Nエージェントの非協力ゲームにおいて, インセンティブの合計が0であるという条件のもと, 不安定なナッシュ均衡の安定化が可能である. 擬似勾配ゲームの感度が未知の場合であっても, 適応制御を用いて不安定なナッシュ均衡の安定化を行うことができる. 適応制御を用い, インセンティブのパラメータの更新則を設計した.
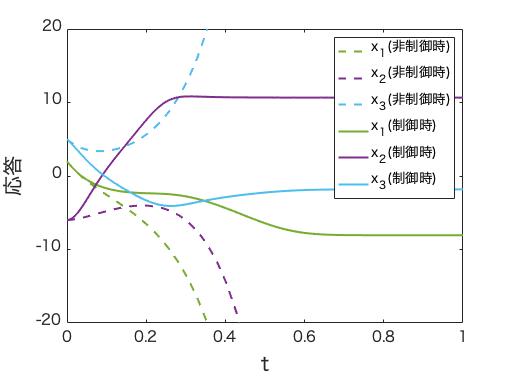 |
| 非協力ゲームのシステムでのエージェントの振る舞い. エージェント数は3, エージェントの状態をxとする. 不安定なナッシュ均衡に対して, 非制御時は遠ざかる(破線)が, 制御によって収束する(実線). |
参考文献
[1] Nash, J. (1951). Non-Cooperative Games. Annals of Mathematics, 54(2), second series, 286-295. doi:10.2307/1969529
[2] J. B. Rosen. Existence and Uniqueness of Equilibrium Points for Concave N-Person Games. Econometrica, Vol. 33, No. 3, pp. 520-534, 1965.
[3] J. S. Shamma and G. Arslan. Dynamic fictitious play, dynamic gradient play, and distributed convergence to nash equilibria. IEEE Transactions on Automatic Control, Vol. 50, No. 3, pp. 312– 327, March 2005.
[4] M. Dindoš and C. Mezzetti. Better-reply dynamics and global convergence to nash equilibrium in aggregative games. Games and Economic Behavior, Vol. 54, No. 2, pp. 261–292, 2006.
[5] T. Alpcan, L. Pavel, and N. Stefanovic. A control theoretic approach to noncooperative game design. In Proceedings of the 48h IEEE Conference on Decision and Control (CDC) held jointly with 2009 28th Chinese Control Conference, pp. 8575–8580, Dec 2009.
[6] T. Kanazawa, T. Misaka, T. Ushio, and Y. Fukumoto. A control method of selfish routing based on replicator dynamics with capitation tax and subsidy. In 2009 IEEE Control Applications, (CCA) Intelligent Control, (ISIC), pp. 249–254, July 2009.
[7] K. Takafumi, M. Takurou, and U. Toshimitsu. A control method of dynamic selfish routing based on a state-dependent tax. IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences, Vol. 96, No. 8, pp. 1794–1802, 2013.
[8] Y. Yan and T. Hayakawa. Stability and stabilization of nash equilibrium for noncooperative dy- namical systems with tax/subsidy approach. Preprint submitted to Automatica, 2019.