物理学や生態学においてカオス現象を内包するモデルは多数知られている．カオス現象は，初期値がわずかに異なるだけでその後の挙動が全く異なるという性質をもっており，短期的な予測は可能であっても長期的な予想は不可能となるような現象である．たとえば，大気循環のモデルとして有名であるLorentz方程式[1]はカオス現象の例であり，これは天気予報が当たらない原因になっているといわれている．すなわち，演算機が無限の精度で計算できないことによる初期値の誤差が，大気循環モデルの初期値鋭敏性によって未来の状態の予測結果に大きな影響を及ぼすため，天気予報が当たらないのである．このようにカオス現象は非常に身近な存在である．これらのカオスモデルを理解するにあたり，カオスの発生原理を調べることが重要視されている．

そこで，先行研究において単純なカオスのモデルとして正三角形折り畳み写像[2]が提案されている．本研究では，単純なカオスモデルを解析することでカオスの発生メカニズムを調べることを目的としている．

ところで，カオスの発生メカニズムの研究として，馬蹄写像[3]の研究が挙げられる．馬蹄写像は，「van der pol振動子[3]のカオス的な挙動は相空間が馬蹄構造を有していることが原因である」という考えから発生した写像である．また，馬蹄構造とは，「系の発展にしたがって，相空間内にとった長方形の空間が馬蹄状に曲げられる構造」のことである．このような馬蹄構造を持つ力学系はカオス的な振る舞いを示すことが分かっており，馬蹄構造が縮小空間と拡大空間を両方兼ね備えていることが，カオス的振る舞いの原因であるといわれている．

一方で，正三角形折り畳み写像は縮小空間を持たず，拡大空間のみ持つ(これを正三角形折り畳み写像的な構造と呼ぶこととする)．そこで，正三角形折り畳み写像が拡大空間しか持たない系をモデル化したものであると考え，拡大空間しか持たないカオスシステムのその振る舞いの原因が，正三角形折り畳み写像的な構造を持っていることと関連性があると考えることができる．この観点にたって考えるならば，正三角形折り畳み写像の発展性は多岐にわたる．なぜならば，未だに解明されていない複雑な振る舞いを示す力学系の振る舞いの原因の理解への契機を与えると考えられるためである．

正三角形折り畳み写像の具体的な解析手法としては，分岐解析を用いる．先行研究において定数として扱われていた値を分岐パラメータとして再定義し，分岐解析をおこなうことで正三角形折り畳み写像におけるカオス的振る舞いの原因の考察をおこなう．たとえば，ロジスティック写像[4]では，パラメータを徐々に大きな値にすると有限のパラメータに達するまでに周期軌道が無限回周期倍分岐し，パラメータがその値から他のある値に達するまでカオス的な挙動を示す．正三角形折り畳み写像におけるカオスの発生メカニズムがロジスティック写像におけるカオスの発生メカニズムと同じであるとは限らないが，周期軌道の分岐が正三角形折り畳み写像におけるカオスを引き起こす一端を担っていることや，パラメータのある範囲ではカオス的であるが，ある範囲ではカオス的ではないといった性質を持つことは予測できる．そこで，分岐パラメータを変動させたときの周期軌道を調べ，カオス的振る舞いとの関連性を探る．

カオス現象

カオス現象とは非線形の力学によって生み出される複雑かつ予測不可能な挙動を表す現象である．研究者によってカオスの定義は異なるが，カオス現象と銘打たれるものには共通した性質がある．具体的には，相空間内のある不変集合において力学系がカオス的であるとは，

1. 初期値に対する敏感な依存性を持つこと．たとえば，Lyapunov数[5]や位相的エントロピー[6]によって定量化される．
2. 不変集合が有界な閉不変集合であること．
3. 分解不可能性をもっていること．これは系を部分形に分割することができないことを意味し，位相推移性や鎖推推移性[7]によって表現される．

の性質を力学系が持っていることである．カオスの具体的な定義に，リ・ヨークの定義[8]やDevaneyの定義がある．先行研究では正三角形折り畳み写像がDevaneyの意味でカオス的[9]であることを示している．Devaneyの意味でカオス的とは，力学系が

1. 位相推移的な性質をもつこと
2. Guckenheimerの意味で初期値鋭敏性をもつこと[3]
3. 周期軌道が不変集合内で稠密であること

正三角形折り畳み写像の定義と数式的表現

正三角形折り畳み写像を定義する．まず，図1に示した，正三角形の領域を折り畳む操作(1)，回転する操作(2)，拡大する操作(3)を考える．この一連の操作によって，正三角形の領域は，元と大きさと向きが同じ正三角形の領域となる．このとき，あらかじめ領域上に点を定義していたときの点の遷移に対して正三角形折り畳み写像と定義している．

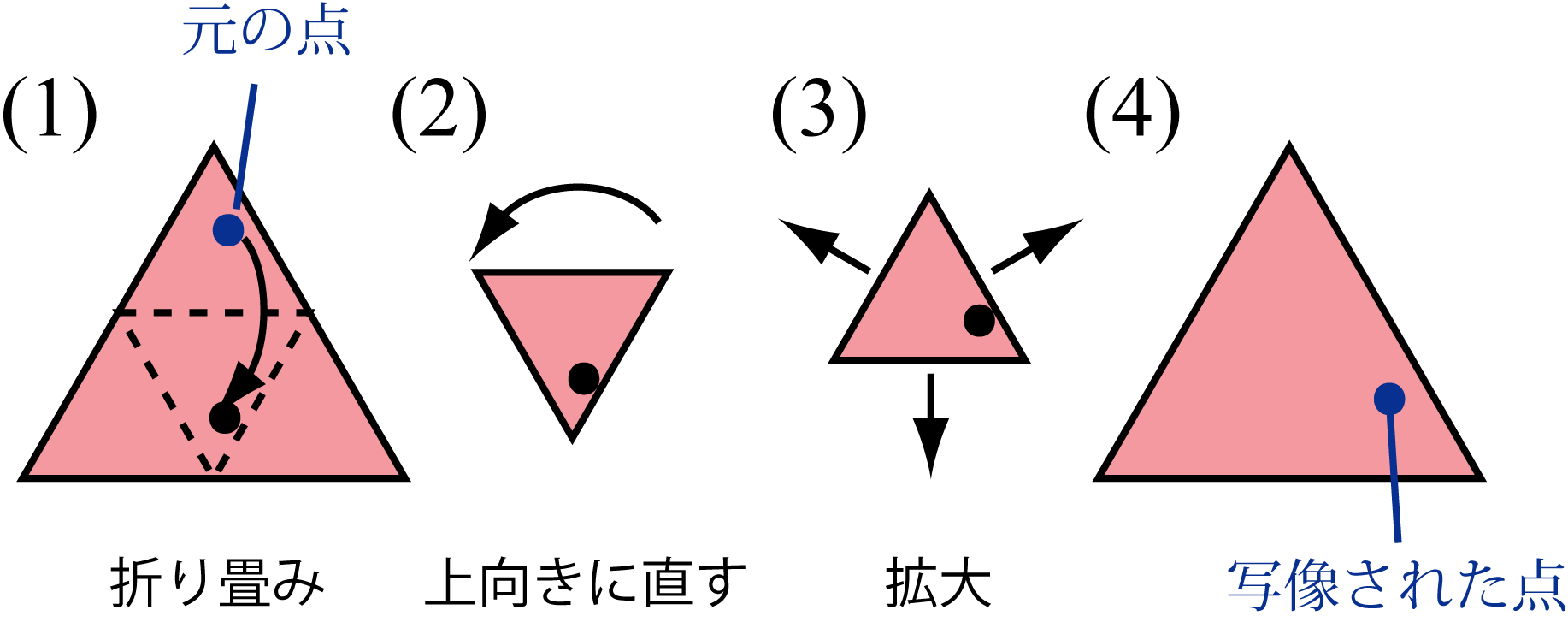図1: 正三角形折り畳み写像

操作(2)は60度回転，180度回転，鏡像変換などの複数の方法が考えられるが，これらを網羅的に調べることは本質的ではない．なぜならば，正三角形折り畳み写像は折り畳みと引き伸ばしという二つの簡単な操作の組み合わせであるにもかかわらずカオス的な挙動を示すことが重要であると考えられるためである．

正三角形折り畳み写像を数式モデルによって表現する．具体的には60度回転，180度回転，鏡像変換の操作が考えられる．しかし，これらの操作を網羅的に調べるのは本質的ではない．なぜならば，正三角形折り畳み写像の本質は折り畳み操作と引き伸ばし操作にあるためである．そこで図2の同値類を導入する．

図2: 同値類

すなわち，正三角形領域上に二点を取り，どちらか片方の点に重心周りにおける120度回転，重心周りにおける-120度回転，重心を通る軸における鏡像変換のいずれかを作用させることでもう一方の点に重なるとき，これらの二点を同値であると見なしている．正三角形折り畳み写像の定義域を図の紫の領域に制限し，かつ図1の操作の最後に「図2の紫の領域に属している同値な点に移す操作(図3)」を加えれば，図の紫の領域が正三角形折り畳み写像の定義域となり，値域となる．

図3: 同値類による点の移動

つぎに正三角形折り畳み写像を数式によって表現する．まずは図4(a)のように座標軸を設定する．紫の領域は正三角形折り畳み写像における定義域であり，値域である．

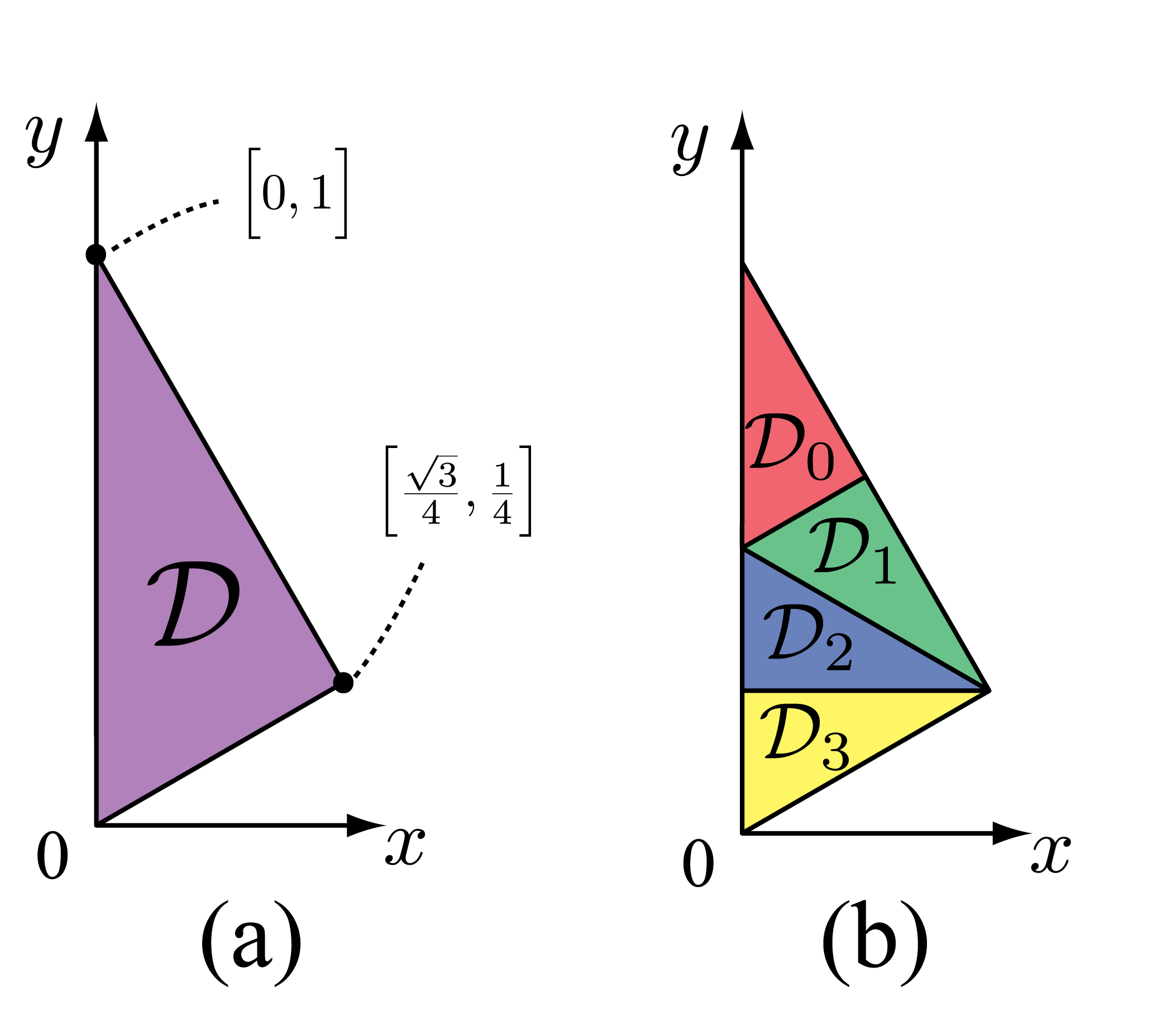図4: 正三角形折り畳み写像における座標の設定と区分の表示

このとき，正三角形折り畳み写像は区分Affine変換であり，定義域は図4(b)のように4つの領域に分割され，それぞれの領域に対して別々のAffine変換が割り当てられる．このようにして定義された正三角形折り畳み写像はDevaneyの意味でカオス的である．

分岐パラメータとしての拡大率の導入

分岐パラメータとして拡大率を定義する．図1における操作(3)を再定義し，拡大率を2倍ではなく1倍から2倍の間の任意のa倍によって再定義する(図5)．この拡大率という分岐パラメータは，引き伸ばしの度合いをパラメタライズしたものであり，拡大率に関する解析をおこなうことで引き伸ばし操作がカオス的挙動にどのような影響を与えているのかを知ることができると考えられる．

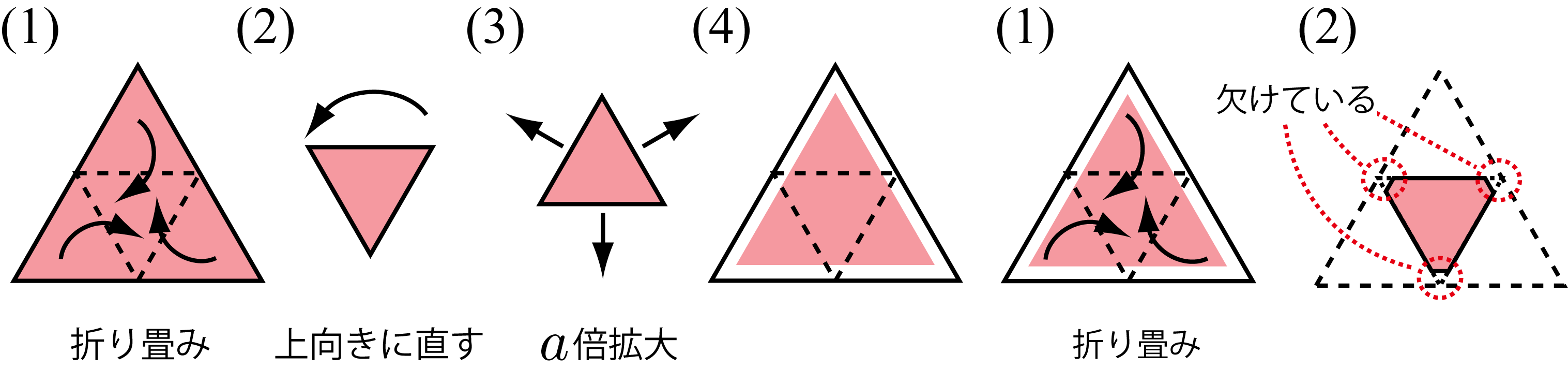図5: 拡大率の定義

注意点は，拡大率aで拡大した正三角形を折りたたむときに，折りたたんだあとの領域が正三角形でなく六角形になることである．拡大率aを導入した正三角形折り畳み写像も拡大率2倍の正三角形折り畳み写像と同様に区分Affine変換である．このときの定義域，値域が図6(a)，区分が図6(b)である．

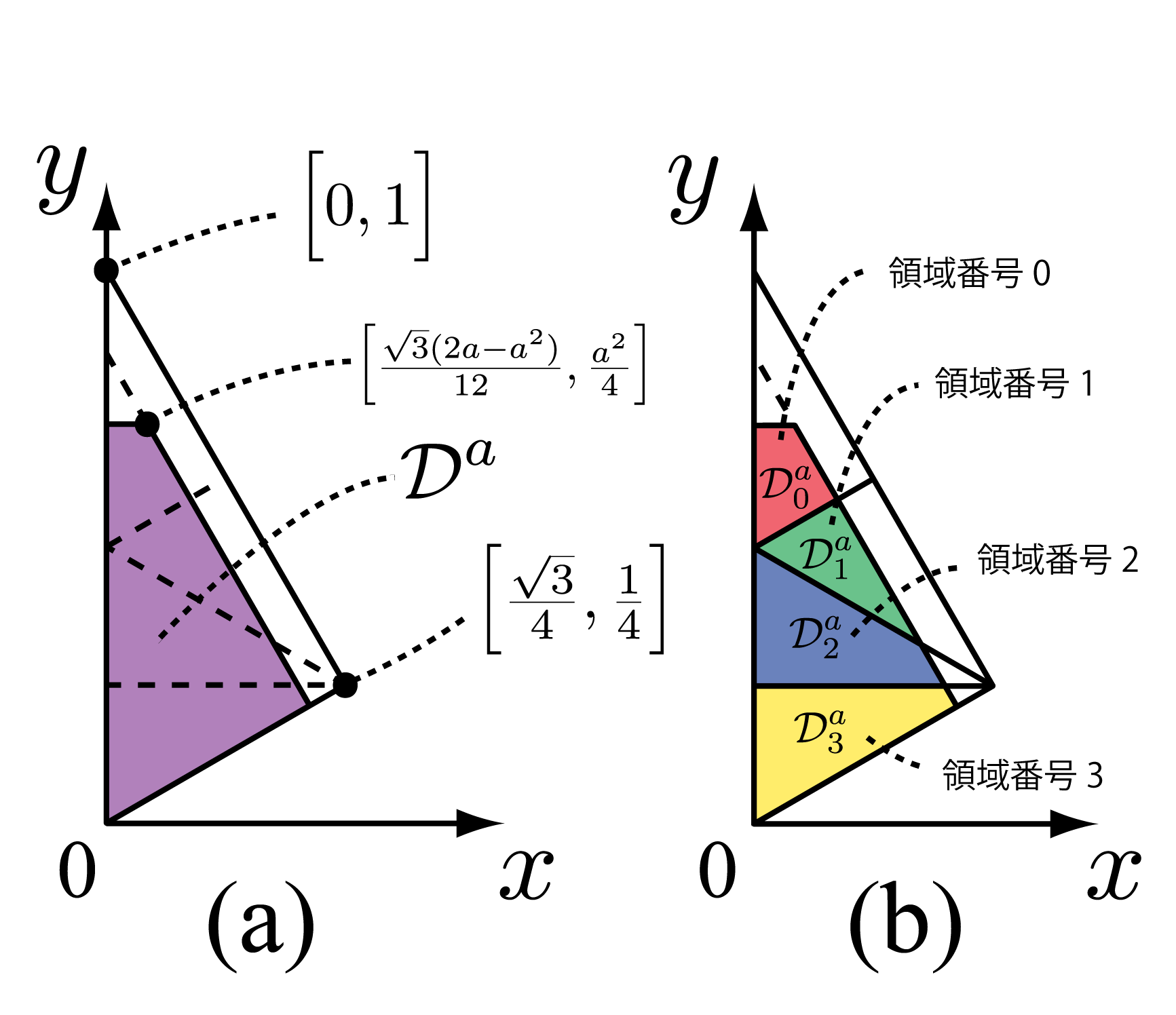図6: 拡大率を導入した正三角形折り畳み写像における定義域，値域，区分の表示

このようにして拡大率を導入し，適当な初期点に複数回正三角形折り畳み写像を作用させたときの定常状態を調べると，図7のようになる．

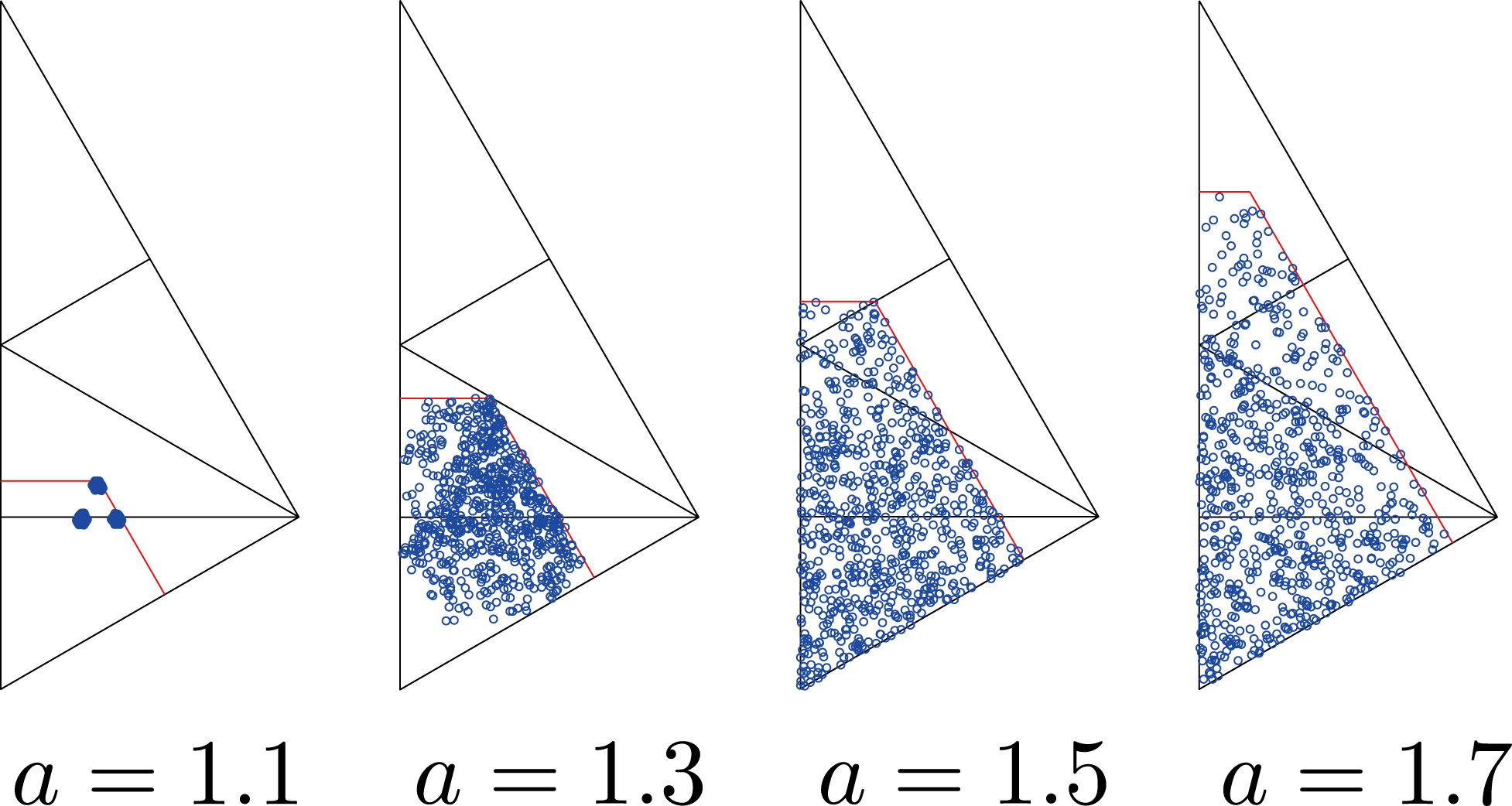図7: 拡大率1.1倍，1.3倍，1.5倍，1.7倍のときの系の振る舞い

図7では拡大率が1.1倍のときは三周期軌道のようなアトラクタが発生し，徐々に拡大率の値を大きくしていくにしたがいアトラクタがばらけていく様子がわかる．このような拡大率によって系の振る舞いがかわる原因を調べるため，本研究では周期軌道の解析をおこなう．

任意の周期軌道において成り立つ性質

正三角形折り畳み写像は区分Affine変換であり，図6(b)の区分となっていることは先述した．ここで，周期軌道がどの順序で領域を遷移するかによって周期軌道を分類する．たとえば，領域番号0,1,2,0,1,2,0,1,2,・・・の順序で領域を遷移する周期軌道を考える．この周期軌道の周期的遷移領域列を{0,1,2}と表記することとする．じつは，一つの周期的遷移領域列に対して，対応する周期軌道は高々一つであることを証明することができる．すなわち，{0,1,2}に対応する周期軌道は高々一つしか存在しない．よって，周期的遷移領域列{0,1,2}に対応する周期軌道は{1,2,0}，{2,0,1}の周期的遷移領域列に対応する周期軌道と同じである．

正三角形折り畳み写像における分岐

シミュレーションによって確認された性質について説明する．正三角形折り畳み写像は，「任意の周期的遷移領域列に対して一つの拡大率(以後境界拡大率と呼ぶ)が定まり，その拡大率より値が大きい拡大率ではその周期的遷移領域列に対応する周期軌道が存在し，値が小さい拡大率では存在しない」性質を持つ．

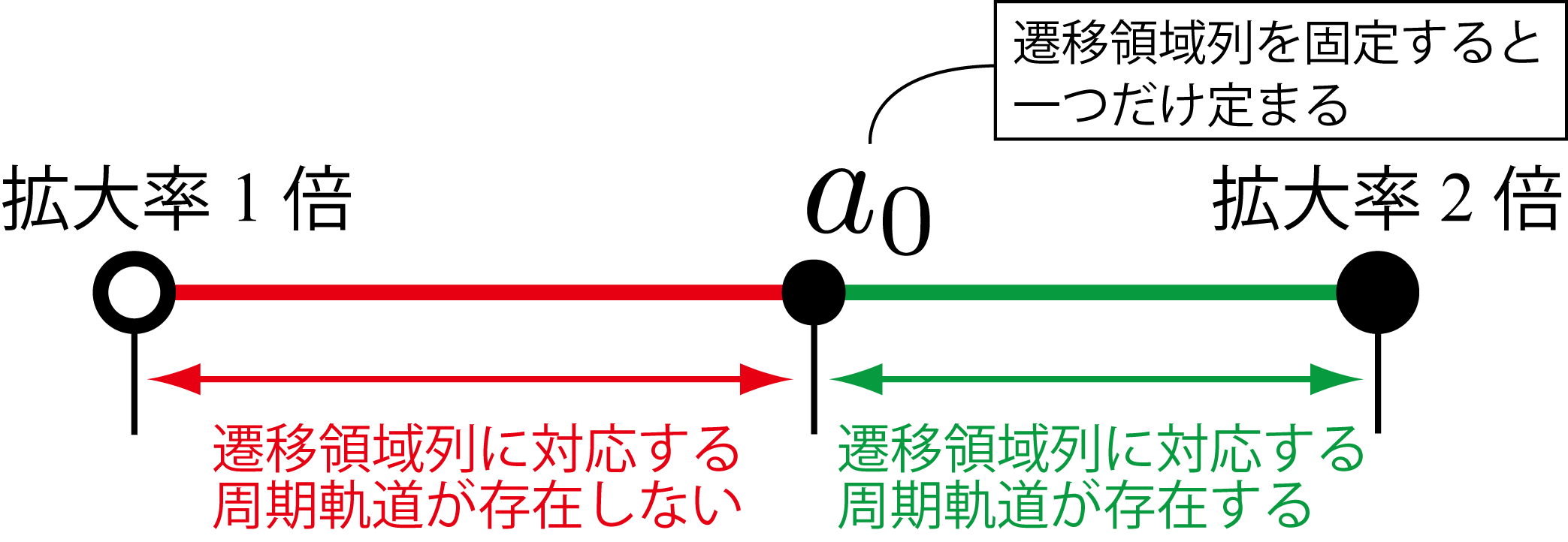図8: 任意の周期軌道の存在する拡大率の範囲

すなわち，拡大率の値を1倍から徐々に大きくしていくとき，境界拡大率においてそれまで存在しなかった周期軌道が発生すると見ることができる．このようにあるパラメータにおいて周期軌道の個数が変化する性質は分岐のもつ性質と一致するので，この現象を分岐[10]と呼ぶ．また，正三角形折り畳み写像における分岐は特殊な性質を持っていることがある．周期的遷移領域列{1,2}，{1,3}に対応する周期軌道の拡大率に関する軌跡を表示したものが図9である．

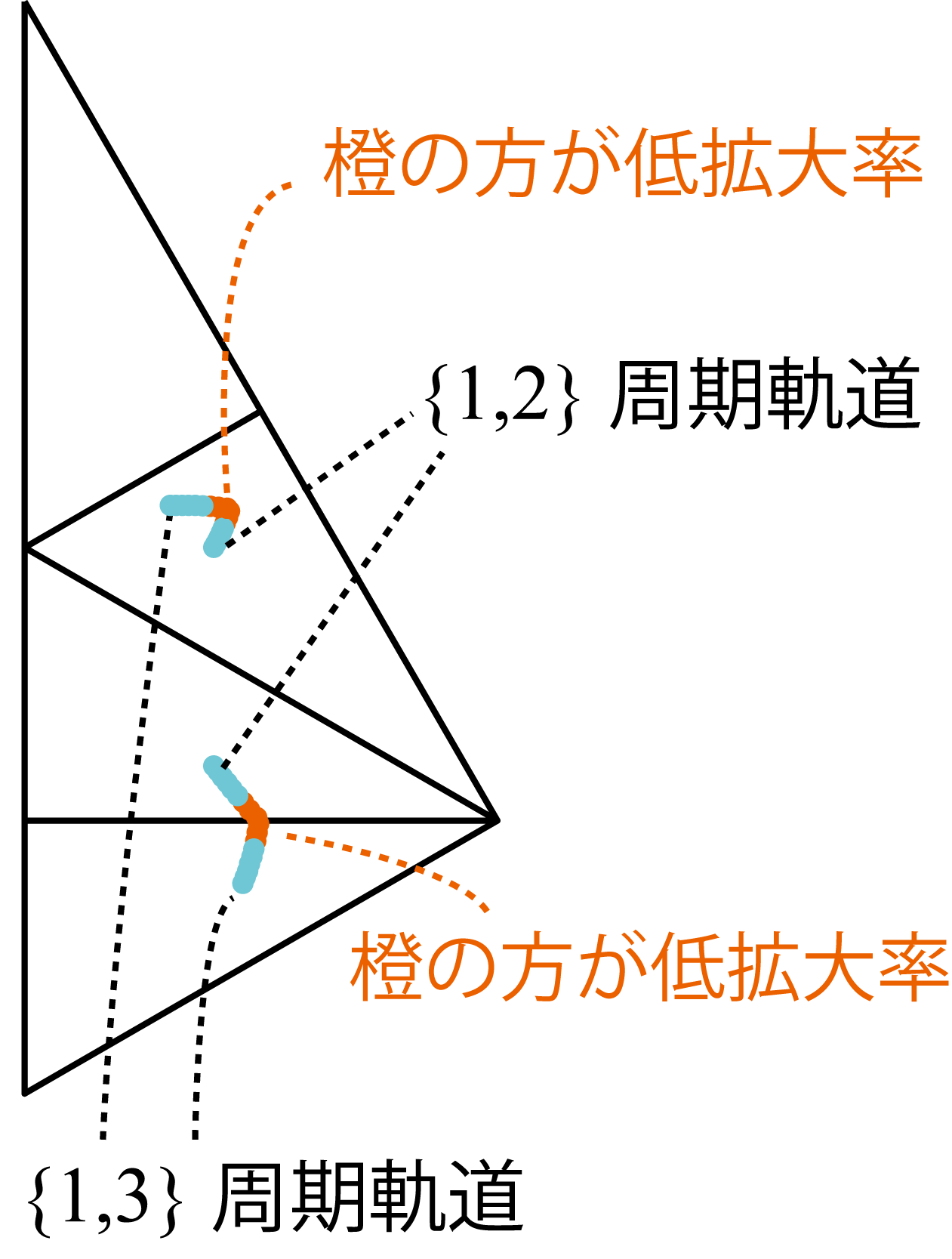図9: 周期的遷移領域列{1,2}{1,3}に対応する周期軌道の拡大率に関する軌跡

このとき，周期的遷移領域列{1,2}{1,3}に対応する周期軌道の境界拡大率は同じで，1.7221…である．この拡大率より大きい値の拡大率であれば対応する周期軌道が存在する．さらに，境界拡大率において周期的遷移領域列{1,2}，{1,3}に対応する周期軌道が発生するときこれらの周期軌道の座標も一致する．以後この座標を境界座標と呼ぶ．このように，異なる周期的遷移領域列を持っているにもかかわらず境界拡大率と境界座標が同一になるような現象は，分岐の中でも特殊なケースであると考えることができる．同一の境界拡大率と境界座標を持つような複数の周期的遷移列S1，S2，…，Snに対して，「S1,S2,...,SnはクラスFの分岐である」という言葉を以後用いる．この現象は正三角形折り畳み写像の折り畳み操作による現象であると考えられるので，Foldingの頭文字にちなんでクラスFとしている．シミュレーション上では，ほとんどの周期的遷移領域列に対してある周期的遷移領域列が存在し，その周期的遷移領域列とクラスFの分岐となっている．存在条件が拡大率によらず存在するような周期的遷移列はクラスFにはならない．さらにクラスFの分岐にはフラクタル的な特徴がある．複数の異なる周期的遷移領域列がクラスFの分岐であるとき，これらの周期的遷移領域列を任意の順序でつなげて周期的遷移領域列を作るとき，新しく作られた周期的遷移領域列もこれらとクラスFの分岐である．たとえば，周期的遷移領域列{1,2}，{1,3}ならば，{1,2}，{1,3}を任意につなげた列も{1,2}，{1,3}とクラスFの分岐である．もっとも簡単な例として{1,2,1,3}に対応する周期軌道を図示したものが図10である．

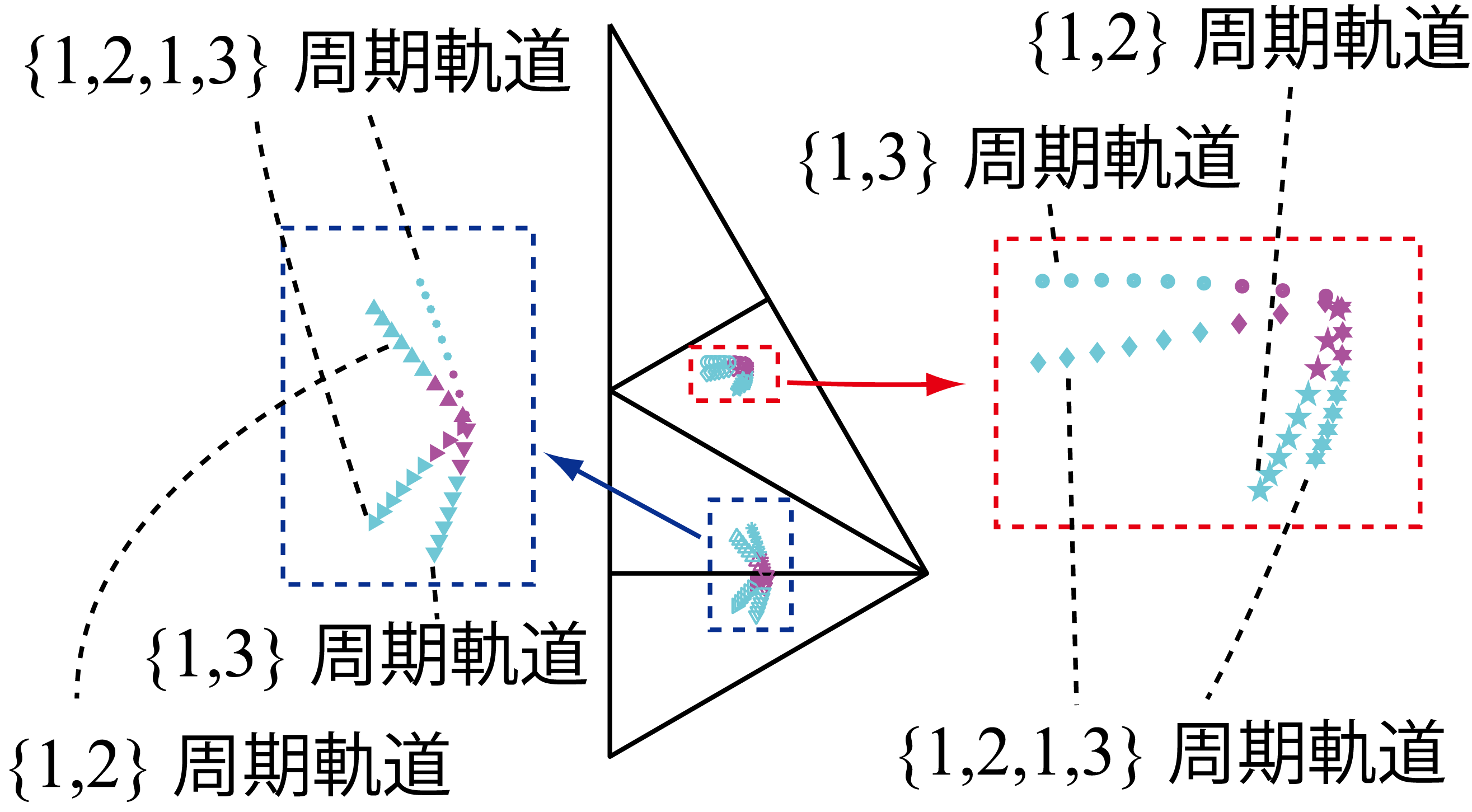図10: 周期的遷移領域列{1,2}，{1,3}，{1,2,1,3}に対応する周期軌道の拡大率に関する軌跡

拡大率を境界拡大率より少し大きくとったうえで{1,2}，{1,3}を任意に組み合わせて作ることの出来るあらゆる周期軌道の座標を調べる．すなわち，{1,2}，{1,3}，{1,2,1,3}，{1,2,1,2,1,3}，{1,2,1,3,1,3}，{1,2,1,2,1,2,1,3},・・・に対応する周期軌道の座標を調べる．ただし，すべての周期的遷移領域列を調べることは計算量に限界があるため無理であるので，十分大きな周期までの周期的遷移列を調べる．この結果が図11である．

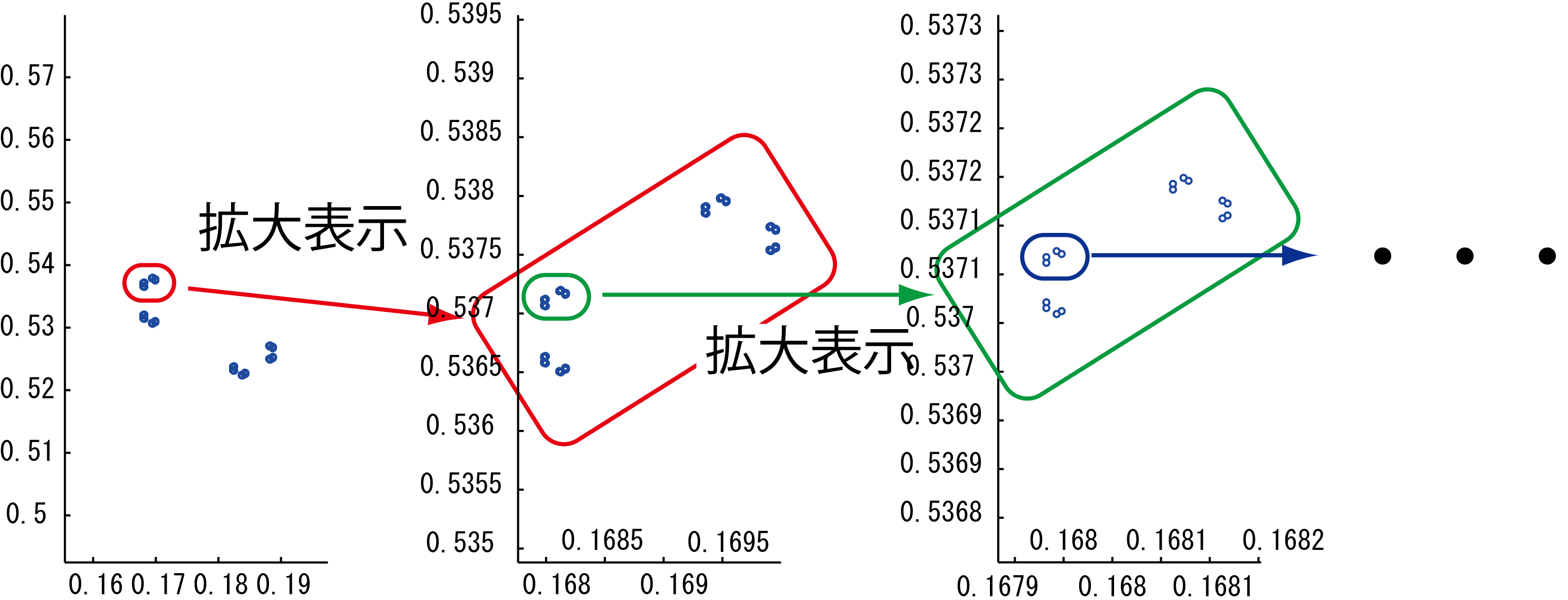図11: クラスFの分岐のフラクタル構造

ただし，ここでいうフラクタル構造[11]とは，「周期軌道の座標が4つのパッケージから構成され，そのパッケージを拡大すると4つのパッケージから構成され，さらにそのパッケージを1つ取り拡大すると4つのパッケージから構成され，・・・」という性質にたいしてフラクタル性という表現を用いている．論文では，これらの性質を，記号力学を用いることによって考察している．

正三角形折り畳み写像における分岐図

分岐図とは，平衡点や周期点の座標を縦軸に，パラメータを横軸に取った図である．たとえばロジスティック写像であれば，図12のような分岐図を得られる．

図12: ロジスティック写像の分岐図

ロジスティック写像ではパラメータを徐々に上げていくと有限のパラメータに達する前に無限回の周期倍分岐をおこし，カオス化する．正三角形折り畳み写像においても，このような分岐図を書く．ロジスティック写像における周期軌道は安定であり，数値的に計算することが可能であるが，正三角形折り畳み写像では周期軌道が安定でないため数値的に捕捉することは難しい．したがって周期軌道の捕捉は解析的に行わざるをえず，あらゆる周期軌道を捕捉することは不可能である．そこで，正三角形折り畳み写像のある周期の周期軌道のみを求め，分岐図を描く．また，正三角形折り畳み写像は二次元のシステムであるため，分岐図が三次元となる．実際に固定点，2,3,4周期軌道について分岐図を描いたものが図13である．

図13: 正三角形折り畳み写像の分岐図

この図より，拡大率を低くとった場合には周期軌道の多くが消滅すると考えられ，低拡大率時には周期軌道が相空間内に稠密に分布しないであろうことも推測される．これは正三角形折り畳み写像が低拡大率において，Devaneyの意味でのカオスではなくなることを意味し，拡大率が正三角形折り畳み写像のカオス性に影響を与えていることを意味する．

正三角形折り畳み写像における分岐現象とカオス性の関連性を調べていく．具体的には，任意の拡大率の正三角形折り畳み写像がカオス的であるかどうかを調べていく．先述したように，Devaneyの意味でのカオスとは，「周期軌道が相空間で稠密であること」「位相推移的であること」「Guckenheimerの意味で初期値鋭敏性をもつこと」の3条件を満たすことである．先行研究によると1つ目と2つ目の条件から3つ目の条件を証明することが可能であるので，[12,13]1つ目の条件と2つ目の条件を任意の拡大率の正三角形折り畳み写像において調べていく．今回は説明しなかったが，フラクタル性をもった分岐現象について，論文では記号力学を用いて考察している．正三角形折り畳み写像の位相推移性についてはこの記号力学系[7]を用いて考察を行っていく．

また，拡大率が2倍であるときの正三角形折り畳み写像の不安定周期点の安定化の手法を考える．具体的にはDelayed Feedback Control[14]による制御，あるいはOGY法[15]による制御を考えている．次に，任意の拡大率の正三角形折り畳み写像の周期点の安定性を調べ，不安定であるならば安定化手法の考案，安定であるならば安定性が変化するターニングポイントを調べる．最終的には倍率が未知であっても，任意の点を周期軌道上に制御するような制御手法を適応制御により達成させる．