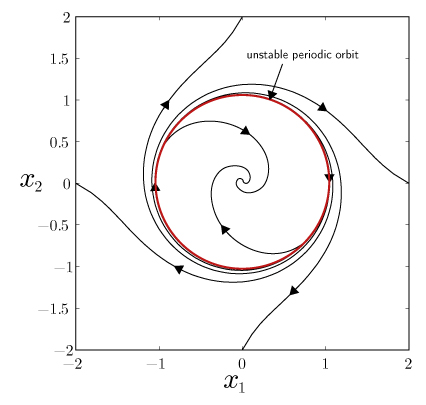
One of the properties that is unique in nonlinear systems is the presence of periodic orbits. The system state stays on the limit cycle when its starting point is on that orbit. When changing the initial point slightly away from the orbit results in the variables diverging away, these orbits are called unstable periodic orbits. Figure 1 is an example of a system with an unstable periodic orbit at the unit circle [1]. Conversely, a periodic orbit where the state with the initial points in the neighbourhood of the orbit converges towards the orbit is called a stable periodic orbit. The topic of stabilizing unstable periodic orbits is an important problem in the study of nonlinear systems, particularly in the study of chaotic systems. For instance, generally in chaotic systems, unstable periodic orbits appear in multiple numbers. One of the method that is known to be able to stabilize unstable periodic orbits is the Pyragas method of delayed-feedback control (DFC) [2], also known as time-delay autosynchronization (TDAS). Through this method, the controller's input is fed by the difference between the system's current and delayed state. The period of the unstable periodic orbit is usually taken as the delay time. The reason is, when the system's state reaches the originally unstable periodic orbit, the control input vanishes and hence the system will stay on that orbit. Since through this method no identification of the unstable periodic orbit is required, DFC is simple and convenient. In general DFC can be classified into two types, namely, static and dynamic control [3][4].

Figure 1-1: Phase plot of a nonlinear system with an unstable periodic orbit at the unit circle

Stability Analysis of the DFC

In normal cases, when applying DFC one usually deals with systems with unknown mathematical representation of its system. For a system with an unstable periodic orbit of a certain period, to find a feedback gain that stabilizes that system towards its unstable periodic orbit, various values of feedback gain should be tested on a trial-and-error basis. The result of this is that the mechanism of the DFC itself is poorly understood. Therefore is a need to understand the mechanism of the DFC. That understanding includes the knowledge of the deriving stability conditions for systems treated with DFC. Indeed, several papers including [5-8], suggest stability conditions for systems with unstable periodic orbit using DFC. However, all these conditions involve controlling parameters that are relatively difficult to compute numerically. For instance, in [6] the author suggests a method of stabilizing a nonlinear system with an unstable periodic orbit by changing the sign of the real Floquet exponent acquired from the linear variational equation of the nonlinear system. Through this method, one has to find out the value of the Floquet exponent of the uncontrolled system, and also a comprehension of what is known as 'the coupling mechanism of the controlling force of the controller' before finally constructing stability conditions for the feedback gain.

Act-and-wait concept

In deriving stability conditions for systems treated with DFC, a problem arises from the presence of a delay term in the system that creates a delay-differential equation. Delay-differential equation are difficult to handle because its state space is infinite dimensional. In light of this fact, the act-and-wait concept [9] allows avoiding the matter of addressing the problem as a system with an infinite dimensional state space by reducing the state space to one that is finite dimensional. In this concept, an act-and-wait controller allows the creation of a finite-sized state-transition matrix, thus a monodromy matrix. While the concept was created for linear time-invariant systems, it has never been used on nonlinear systems.

We intend to find local asymptotic stability conditions for a nonlinear system treated with act-and-wait-designed DFC in terms of only the feedback gain in the delayed feedback controller. For convenience, we focus our investigation on nonlinear systems with known mathematical representation containing informations of the unstable periodic orbit's period and its location in the state space. With these conditions satisfied, we need only to linearize the nonlinear system about its unstable periodic orbit, and derivation of the stability conditions is possible from the linearized system.

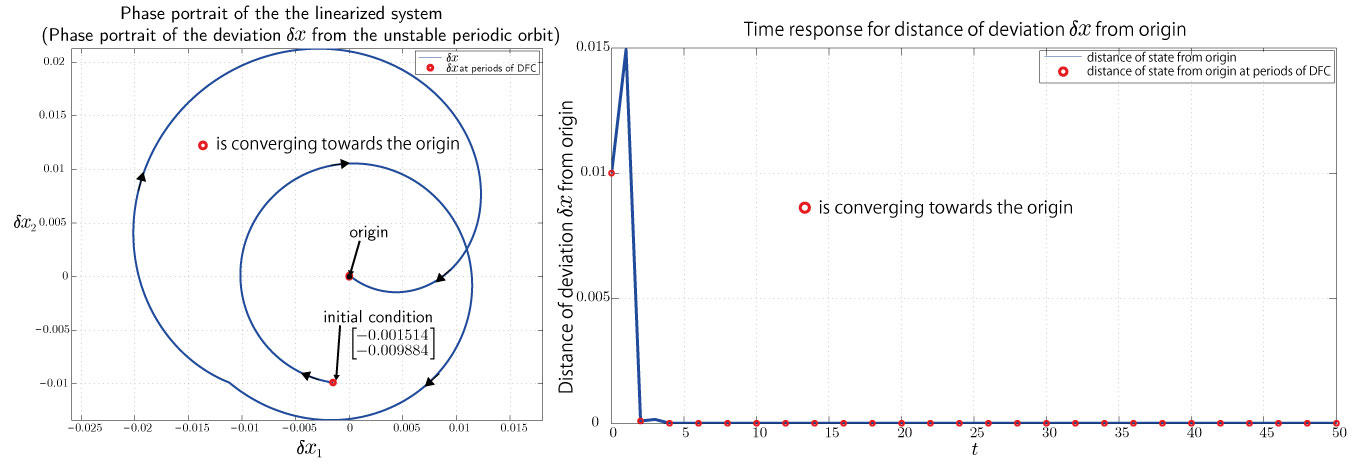
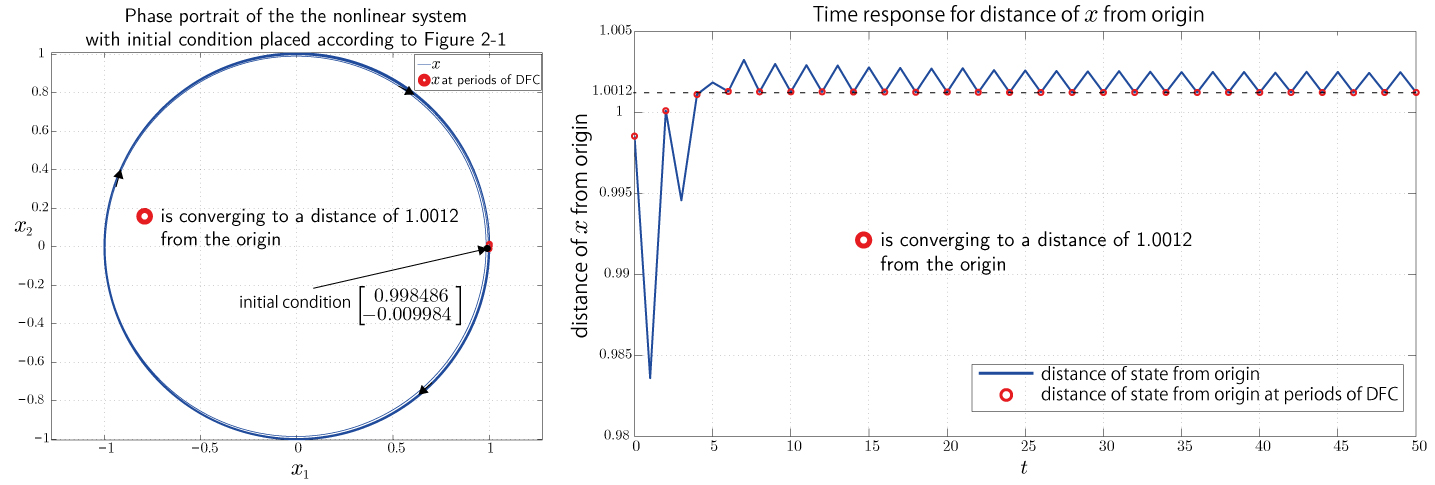
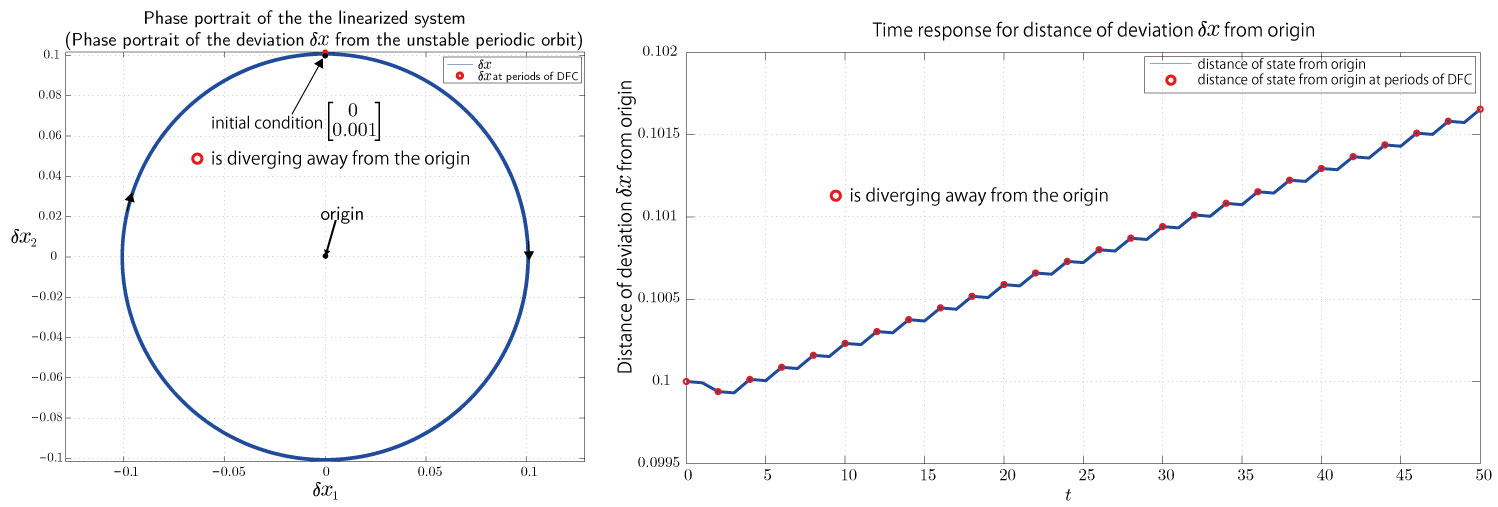
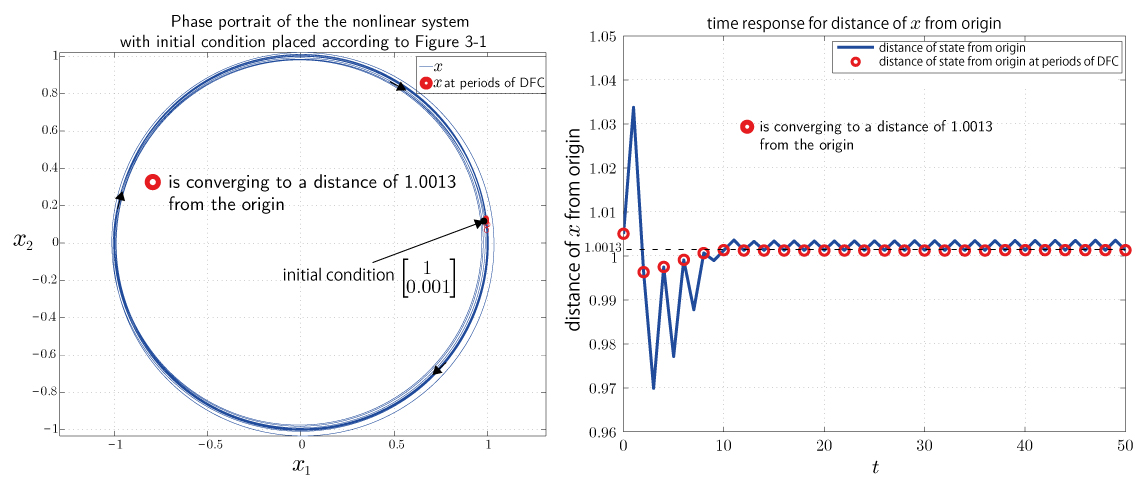
Through linearization about the unstable periodic orbit, the linearized system represents the dynamics of the nonlinear system's state deviation from the unstable periodic orbit.It turns out that the state-transition matrix of the linearized system describes the behaviour of the nonlinear system's state deviation from the unstable periodic orbit. Furthermore, we found that the eigenvalues of the monodromy matrix of the linearized system determines the behaviour of the deviation in the long term.For the nonlinear system to be asymptotically stable towards the unstable periodic orbit, the system's state deviation has to be asymptotically stable towards the origin. In terms of the monodromy matrix, its eigenvalues has to be inside the unit circle of the complex plane. We tested our act-and-wait designed DFC on a nonlinear system with whose unstable periodic orbit is described in Figure 1-1. Unfortunately, the best feedback gains that we could find so far are those that place the eigenvalues of the monodromy matrix respectively near the origin of the complex plane (inside the unit circle) and slightly outside the unit circle. In this case, the linearized system is stable when the initial condition is placed at certain locations (for example, see Figure 2-1) and is not stable otherwise (for example, see Figure 3-1). However, we do not see stabilization when either of these initial conditions are placed accordingly inside the state-space of the nonlinear system (see Figure 2-2 and Figure 3-2). In specific, in both cases the state of the nonlinear system at integer multiples of the period of the act-and-wait designed DFC converges to a certain distance from the origin, but this cannot be considered a 'stable periodic orbit' because if the DFC were to be relieved at any instant this 'stable periodic orbit' appears, the state would eventually diverge away. We believe that this occurrence is due to the effect of the mathematical terms that in the nonlinear system that is neglected in the process of linearization.

Figure 2-1: Phase plot of linearized system with initial condition that brings stabilization

Figure 2-2: Phase plot of nonlinear system with initial condition placed according to that of Figure 2-1

Figure 3-1: Phase plot of linearized system with initial condition that does not bring stabilization

Figure 3-2: Phase plot of nonlinear system with initial condition placed according to that of Figure 3-1

Further work on finding a example of a system with an unstable periodic orbit that can be stabilized by the act-and-wait designed DFC needs to be done. Since the key to be able to apply the act-and-wait designed DFC is to have prior knowledge of the location of unstable periodic orbit of a system, work on acquiring knowledge of the location of the unstable periodic orbit is important. One viable way of doing so is through the use of adaptive control [10].

State-Transition Matrix and Monodromy Matrix [3] [6]

The monodromy matrix is another name for a state-transition matrix at an integer multiple of the period of the periodic orbit. Knowing the monodromy matrix allows us to know the behaviour of the state at a certain time and the state of every following period after that time. Specifically, the monodromy matrix's eigenvalues (also known as Floquet multipliers) and eigenvectors describe the direction of motion of the state at every period.

Floquet Theory

The Floquet exponent is the logarithmic value of the Floquet multiplier. The real part of the Floquet exponent governs the instability of the trajectory around the unstable period, while its imaginary part governs the trajectory's revolution (torsion) [6]. In more detail, the former represents how much the present solution has departed away from the solution of one period before, and the latter represents how much the present solution has revolved around the solution of one period before.
It has been discussed in [6] that only systems with an orbit of finite torsion can be stabilized. This is due to the finiteness of the influence of the controller.

Act-and-Wait Controller [9]

Originally intended to be applied on linear systems with feedback delay associated with infinite poles, it is a delay controller with constant delay that is switched on and off in the intervals 'act' and 'wait'. The result is a system in which its behaviour can be represented in a monodromy matrix with a size equal to the number of states in the linear system.

[1] H. K. Khalil,Nonlinear Systems,Prentice Hall, 2002.

[2] K. Pyragas, "Continuous control of chaos by self-controlling feedback,"Phys. Lett. A 170, pp. 421-428, 1992.

[3] S. Yamamoto, T. Hino, and T. Ushio, “Dynamic delayed feedback controllers for chaotic discrete-time systems,”IEEE Trans. Circuits Systems-I: Fund. Theory App., vol. 48, no. 6, 2001.

[4] 山本,　"遅延フィードバックによるカオス制御,"　数理解析研究所講究録,　1369巻, pp. 212-224, 2004.

[5] H. Nakajima, "On analytical properties of delayed feedback control of chaos,"Phys. Lett. A 232, pp. 207-210, 1997.

[6] W. Just, T. Bernard, M. Ostheimer, E. Reibold, and H. Benner, "Mechanism of time-delayed feedback control,"Phys. Rev. Lett.,vol. 78, no. 2, pp. 203-206, 1997.

[7] O. Beck, A. Amann, E. Scholl, J. E. S. Socolar, and W. Just, "Comparison of time-delayed feedback schemes for spatiotemporal control of chaos in a reaction-diffusion system with global coupling,"Phys. Lett. E, 66, 016213, 2002.

[8] W. Just, E. Reibold, H. Benner, K. Kacperski, P. Fronczak, and J. Holyst, "Limits of time-delayed feedback control,"Phys. Lett. A, 254, pp. 158-164, 1999.

[9] T. Insperger, "Act-and-Wait Concept for Continuous-Time Control Systems With Feedback Delay,"IEEE Trans. Contr. Sys. Tech.,vol. 14, no. 5, pp. 974-977, 2006.

[10] K. J. Astrom and B. Wittenmark,Adaptive Control,Dover Publications Inc., 1995.