はじめに
道路交通網やインターネットなどのネットワークを移動する自動車やパケットなどの移動体を効率よく移動させる(移動時間の短縮)ことは,物流や情報の伝達など様々な面で重要である. そのための手段の一つとして,ネットワーク中に新たに道路やケーブルなどの流路を造ることが考えられる. しかしながら,移動時間の短縮を目的としてネットワーク中に新たに流路を造ったにもかかわらず,移動時間の短縮どころか逆に移動時間が増加する現象を招いてしまうことがある[1]. この現象は,直観的には効果がありそうだが実際には逆効果であることが逆説的に感じることから「ブライスのパラドクス (Braess's Paradox)」とよばれ,主に静的なモデルを用いて研究が行われている. しかながら,実際のネットワークの流れは流入流出などが存在し,流量が時間とともに変化する動的な流れであるため,静的モデルでは現実の流れをよくモデル化しているとは言い難い面もある. そこで本研究ではネットワークの流れを動的にモデル化し,静的モデルにおけるブライスのパラドクスに似た現象が起きるかについて解析を行う.
ブライスのパラドクス
利己的な経路選択
道路交通網やインターネットなどのネットワークを移動する自動車やパケットなどの移動体は,一般的にそれぞれの移動体自身の移動時間が最小になる経路を選択することが多い. ネットワークのモデルでは経路ごとに移動コスト関数(移動時間)を定義し,各移動体は自身の移動時間が最小になる利己的な経路選択を行うと仮定している. 利己的な経路選択(selfish-routing)とはゲーム理論の非協力戦略ゲームにおける最適戦略をネットワークにおける経路選択に適用したものである. ゲーム理論における最適戦略とは各移動体は他の移動体の戦略に対して自身の移動時間が最小になるように自身の戦略を決定することである. 非協力戦略ゲームでは,最適戦略である戦略を決定するとナッシュ均衡に戦略が収束する. このときの戦略は,各移動体は自身の移動時間が他の移動体と同じであり,かつ自分一人が経路を変更したとしても自身のコストが減少しない平衡点となる.
移動体が利己的な経路選択をする場合,Pigouの例題[2]で示されるように社会全体(全移動体の平均移動時間)でみると全移動体の平均移動時間が最小(最適)ではない場合がある. つまり利己的な経路選択をする場合,全移動体の移動時間は平等ではあるが,全移動体の平均移動時間は最小にはならず非効率な状態になることが起きる. 一方,社会全体で最適な経路選択は文献[3-6]にあるように利用者全員の平均移動時間の最小化など,評価関数の最適化問題の解として与えられる. 社会全体で最適な経路選択の場合,各利用者の移動コストに差が出ることがある. これは社会全体の利益(効率)のために誰かが犠牲になる状況を表している.
ブライスのパラドクス
利己的に経路を選択する移動体がネットワーク中の地点Aから地点Bまで移動することを考える.このとき,利己的な選択で得られた経路は社会全体で最適であるとする. ここで,ネットワーク中に新たに流路を付け加える.新たに流路を付け加えたネットワークでは社会全体で最適な状態にならない,すなわち全体の平均移動時間が大きくなる場合がある. この状況をブライスのパラドクス(Braess's Paradox)と呼ぶ. 平均移動時間を減少させる目的で新たに経路を加えたにもかかわらず逆に平均移動時間が増加することが直観に反しているようにみえることからこの状況はパラドクスであるといわれており,実際の道路でもこの現象は確認されている[7]. 逆にいえば,経路上にある余計な道を取り除く,あるいは流量を制限することで利用者の移動コストを減らすことができる場合があることを示しており,そのための研究がおこなわれている.
先行研究
静的モデル
ブライスのパラドクスに関する研究はBraessが最初に明示した静的なモデルで多くの解析が行われている. 特に社会全体で最適な場合の移動コストに対する非最適な場合(パラドクスが起きた場合)の移動コストの割合をprice of anarchyとよび,ネットワークの性能劣化の指標として用いられている[8]. 文献[9-11]ではBraessが最初に示したグラフ構造(ブライスグラフ)に対して解析している. 文献[9]ではフロー総量を変化させたときの平均コストの変化に対して解析している. 文献[10]では一般の線形コスト関数でのパラドクスの存在条件を求めている. 特にフロー総量を減らすと全体のコストが増加する場合があるというパラドクス的な結果が出ている. 文献[11]ではコスト関数とフロー需要の関係からパラドクスが存在する条件を求めている.
文献[12]では一般のネットワークに拡張してパラドクスが存在する十分条件を一般の線形コスト関数に対して求めている. 文献[13]ではネットワークに新たにリンクを加えた場合の平均コストの変化量を求めている. 文献[14,15]ではブライスのパラドクスが起きた場合のprice of anarchyの大きさについて議論している. 文献[16]ではコスト関数とフロー量に上限を設定したモデルを用いてパラドクスが起きる条件を求めている. 文献[17]では線形・非線形コスト関数の一般ネットワークについてパラドクスを起こすリンクを取り除くための近似アルゴリズムの近似率を求めている. 以上の研究では各情報(人数,コスト等)は利用者全員が正確に知ることができることを前提としている.これに対して[18,19]では情報伝達の遅れ時間や人数等の不確かさを考慮してprice of anarchyの大きさについて議論している. 他にも,ネットワークの問題だけではなく機械的な構造や電気回路などでもこの現象が生じることがある[20]. 文献[21]では災害時における建物内からの避難に対して,避難者に指示を与えるのではなく建物内のいくつかの通路を封鎖することで避難時間の短縮を狙っている. 通路を封鎖するにあたってブライスのパラドクスの考えを用いている.
動的モデル
前述のブライスのパラドクスに関する研究ではその多くが静的なモデルで解析を行っている.それに対し動的なモデルを用いた研究は少数である. その一つに渋滞を考慮した動的な交通モデルに関した研究がある[22-24]. これらの研究では,流路の容量を増加することによって移動時間が増えるブライスのパラドクスに類似した現象が起こることが確認されている. 文献[8]ではselfish routingを進化ゲームにおけるレプリケータダイナミクスを用いてモデル化している. レプリケータダイナミクスとは進化ゲームにおいて,ある戦略をとる生物が時間とともにどのように発展あるいは淘汰されていくかを知るためのモデルである. 文献[25]では,移動コストの他に人頭税と補助金を用いることによって流量を制御し性能劣化を防ぎ,全体最適な流れを達成している. 文献[26]では移動体の量を時間の関数としてブライスのパラドクスを扱っているがダイナミクスは存在せず,移動体の量の均衡をある不等式から導出することができることを示しており,静的モデルである[11]と同じ結果が導出されることを述べている.
本研究の目的
ブライスのパラドクスに関する研究では動的なモデルを用いたものは前述の研究を含め少ない. そこで,本研究では動的モデルを用いてパラドクス的な現象が起きるのかを調べる. 移動コストを定義しエッジを付け足す前よりもエッジを付け足した後のほうが移動コストが大きくなる場合をパラドクスと定義する. 動的なネットワークの流れのモデルとしてコンパートメントシステムを用いる. コンパートメントシステムとは[27]に示される微分方程式モデルであり質量保存の法則をみたす. そのため,ネットワークの流れを動的に表現するのに適したモデルである. ネットワークの移動コストとして,ダイナミクスの平衡点における線形近似後のダイナミクスの固有値のうち実部が最大な固有値(実部最大固有値)を用いる. ネットワークにエッジを付け足すことで実部最大固有値が増加した場合パラドクスであり,本研究ではパラドクスが起きる条件について解析する.
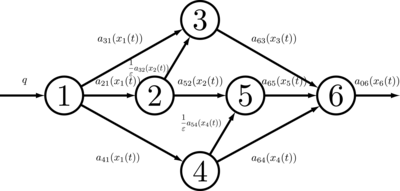
ネットワークの流れの動的なモデル化
コンパートメントシステムを用いてネットワークの流れをモデル化する. 本研究では漸近安定な平衡点における定常的な流れについて解析する. 安定な平衡点を持たない場合,あるノードの状態量が時間の経過とともに増加し続ける,もしくは平衡点から少しでもずれたら状態量が増加し続けることになる.
静的モデルでは移動時間で移動コストを定義しネットワークの性能の指標とすることで各ネットワークの移動コストを比較している. 動的モデルにおいて静的モデルの移動時間に相当するネットワークの移動コストとして,平衡点における線形近似後のダイナミクスの固有値を用いることを考える. ダイナミクスは平衡点で漸近安定と仮定しているので,固有値の実部は負となる. 線形近似後のダイナミクスの解が平衡点に収束する速さは固有値の実部の大きさによって決まる.特に,固有値の実部が最も大きい(0に近い)固有値が収束の速さを表している考えられる. そこで,線形近似後のダイナミクスの固有値のうち実部が最も大きい固有値(実部最大固有値)を移動コストとして用いる.
エッジを付け加える前のグラフをグラフG,エッジを付け加えた後のグラフをG'とする.グラフGの実部最大固有値よりもグラフG'の実部最大固有値のほうが大きいときパラドクスであると定義する.
本研究の結果
Braessが最初に示した4ノードのネットワークに対して流出割合に酵素反応速度論などで用いられるMichaelis-Menten式を用いたダイナミクスではパラドクスが起きることを解析的に示した. また,流入量を変化させることによるパラドクスの発生状況の変化において類似点がみられることを示した.
4ノードのネットワークに対して流出割合を一般の非線形関数を用いた場合においてパラドクスの起きない流出割合の十分条件を導出した. ダイナミクスが線形関数で与えられる場合,任意の有向閉路のないグラフ構造においてパラドクスが起きないことを示した.
グラフ構造を6ノードに拡大した場合にパラドクスが起きることを示した. また,4ノードのグラフ構造の場合において[28]で用いられるている複数のノードの状態量に依存する流出割合を用いたダイナミクスでパラドクスが起きることを示した.
課題
4ノードの場合についてパラドクスが起きる必要条件の導出,グラフ構造を拡大した場合についての解析などがあげられる.
Reference
[1] D. Braess, A. Nagurney and T. Wakolbinger, "On a paradox of traffic planning,'' Transp. Sci., vol. 39, no. 4, pp. 446-450, 2005.
[2] A. Pigou and N. Aslanbeigui, The Economics of Welfare, Transaction Publishers, 2001.
[3] Y. Chiu and P. Mirchandani, "Modeling and optimization of crowd guidance for building emergency evacuation,'' IEEE Int. Conf. Autom. Sci. Eng., pp. 328-334, 2008.
[4] G. Lovas, "On performance measures for evacuatoin systems,'' Euro. J. Oper. Res., vol. 85, pp. 352-367, 1995.
[5] B. Xiong, P. Luh, S. chung, L. Michel and A. See, "Coherent modeling and effective coordination for building emergency evacuation,'' IEEE Int. Conf. Autom. Sci. Eng., pp. 670-677, 2007.
[6] K. Deng, W. Chen, P. Mehta and S. Meyn, "Resource pooling for optimal evacuation of a large building,'' Proc. IEEE Conf. Dec. Cont., pp. 5565-5570, 2008.
[7] G. Kolata, "What if they closed 42nd street and nobody noticed?,'' New York Times, December 25, 1990.
[8] S. Fischer and B. Voecking, "On the evolution of selfish routing,'' Proc. Europ. Symp. Algo., vol. 3221, pp. 323-334, (Bergen, Norway), 2004.
[9] C. Fisk, "More paradoxes in the equilibrium assignment problem,'' Transp. Res., pp. 305-309, 1979.
[10] M. Frank, "The braess pradox,'' Math. Prog., vol. 20, pp. 283-302, 1981.
[11] E. Pas and S. Principio, "Braess' paradox: some new insights,'' Transp. Res., vol. 31, pp. 265-276, 1997.
[12] R. Steinberg and W. Zangwill, "The prevalence of Braess's paradox,'' Transp. Sci., vol. 17, pp. 301-318, 1983.
[13] S. Dafermos and A. Nagurney, "On traffic equilibrium theory paradoxes,'' Transp. Res., vol. 18, pp. 101-110, 1984.
[14] 亀田壽夫, "独立分散最適化によるネットワークにおける性能劣化パラドックスとその大きさ,'' 日本オペレーションズ・リサーチ学会和文論文誌, vol. 48, pp. 26-48, 2005.
[15] M. Englert, T. Franke and L. Olbrich, "Sensitivity of Wardrop equilibria,'' Proc. Spec. Algo. Game Theo., pp. 158-169, (Paderborn, Germany), 2008.
[16] K. Park, "Detecting Braess paradox based on stable dynamics in general congested transportation networks,'' Netw. Spat. Econ., published online, 2009.
[17] T. Roughgarden, "On the severity of Braess's Paradox: Designing networks for selfish users is hard,'' J. Comp. Sys. Sci., vol. 72, pp. 922-953, 2006.
[18] S. Fischer and V. Vocking, "Adaptive routing with stale information,'' Transp. Comp. Sci., vol. 410, pp. 3357-3371, 2009.
[19] I. Ashlagi, D. Monderer and M. Tennenholtz, "Two-terminal routing games with unknown active players,'' Art. Intel., vol. 173, pp. 1441-1455, 2009.
[20] J. Cohen and P. Horowitz, "Pradoxical behaviour of mechanical and electrical network,'' Nature, vol. 352, pp. 699-701, 1991.
[21] 向直人, 渡邉豊英, "災害時における避難者流量の最適化,'' データ工学ワークショップ, E8-6, 2007.
[22] T. Akamatsu, "A dynamic traffic equiliburium assignment paradox,'' Transp. Res., vol. 34, pp. 515-531, 2000.
[23] 桑原雅夫, 赤松隆, "動的ネットワーク解析 -これまでの知見とこれからの展望-,'' 土木学会論文集, no. 653, pp. 3-16, 2000.
[24] X. Zhang, W. Lam and H. Huang, "Braess's paradox in dynamic traffic assignment with simultaneous departure time and coices,'' Transpotmetrica, vol. 4, pp. 209-225, 2008.
[25] T. Kanazawa, T. Misaki, T. Usio and Y. Fukumoto, "A control method of selfish routing based on replicator dynamics with capitation tax and subsidy,'' Nonlinear Anal., vol. 71, pp. e818-e826, 2009.
[26] A. Nagurney, D. Parkes and P. Daniele, "The internet, evolutionary variational inequalities, and the time-dependent Braess Paradox," Comp. Man. Sci., pp. 1-29, 2006.
[27] R. Brown, "Compartmental system analysis: State of the art,'' IEEE Transp. Biomed. Eng., vol. BME-27, pp. 1-11, 1980.
[28] M. Haddad, V. Chellaboina and Q. Hui, Nonnegative and Compartmental Dynamical Systems, Princeton University Press, 2010.