はじめに
森林火災は遥か昔から存在し,植物・生物共に危機をもたらしてきた.
現在,世界では火災によって1日平均1万ha以上もの森林が消失してる. 火災が少ないといわれている日本でも,大小あわせると年間2000件近くの森林火災が発生しており,毎年1000ha以上の森林が消失している[1].
森林内の草木が一度燃え始めると,木々の密集度合いや気温,湿度等の環境によっては炎の燃え広がりが早く,大規模な森林火災へと発展する.
森林火災の威力は絶大であり,消防活動において進歩を遂げてきた今日の技術をもってしても,広範囲に燃え広がった火災を瞬時に消し止めることは不可能である.
そこで近年では,複数のセンサを通して森林を監視し,火災が発生したときに直ちにこれを発見することを目的とした森林監視システムの研究が盛んに行われている.
また,森林火災が起きたときに森林の燃焼状況や炎の温度を赤外線を用いて測定する研究も行われている[25].
このような森林火災の監視・計測を目的とした研究に対して,本研究では複数の消防ビークル(ヘリコプターや消防車)を用いた消火活動を考える.
森林火災が燃え広がる前に,複数の自律ビークルがお互いに連携をとりつつ消火活動を行い,速やかに消火するための制御則を提案する.
また,発見が遅れて火災が燃え広がってしまった時にも,複数のビークルが最適な消火を行うことによって炎の拡散を最小限に食い止め,被害を最小にすることを目指す.
先行研究
森林火災のダイナミクス
森林火災の消火活動を行うためには,まず火災の拡散を正確に予測する必要がある.
森林火災を制御対象と捉え,火災拡散のダイナミクスを導出することで,最適な消火を目的とした制御則を検討できる.
ここでは,近年行われてきた森林火災の拡散を表すダイナミクスに関する研究を紹介する.
森林火災のダイナミクスに関する研究は様々な分野で盛んに行われており,多岐にわたるアプローチが提案されている.
現在までに多くの論文が存在するために,森林火災の拡散のダイナミクスに関する研究のレビューを目的とした論文も存在する[2,3].
これらの論文によると,森林火災のダイナミクスのモデルは二つに大別することができる.
第一に物理的現象からのモデル,第二に数理的モデル(またその両方を統合したモデルもある)である.
物理的現象のモデルとは,草木の燃え方や空気の流れ,熱交換など,ミクロの範囲で物理的に草木の燃焼を解析し,
炎の拡散のダイナミクスを導いたモデルである.
これに対して数理的モデルとは,ミクロのレベルでの炎の解析等は行わず,炎の伝播をマクロな視点で確率的や確定的に捉えることによって,火災の拡散を表したモデルである.
数理的モデルを用いる研究では,さらに多様なアプローチが考えられている.
文献[4,5]では,ホイヘンスの原理(Huygens Principle)を用いたモデルが提案されている.
このモデルでは,時刻 t における火災の境界を考え,微小時間 Δt 後には火災の境界線上の各点を基点として炎が円状に拡散するといったホイヘンスの原理を用いて,
炎の拡散を数理的に表している.
文献[6,7]では,偏微分方程式である拡散方程式を利用した,森林火災の拡散ダイナミクスが提案されている.
また,文献[8-11]では,セルオートマトン(Cellular Automata)を用いたモデルが提案されている.
このモデルでは,森林を小さな格子(セル)に分割し,各セルの状態を考える.
近傍のセルが燃えていたら自分のセルも発火するといった,近傍の状態に依存する確定的なダイナミクスを各セルに与えることによって,炎の拡散を表している.
さらに,いくつかの文献ではパーコレーション理論を用いた手法が提案されている.
文献[12,13,31]では,無限に広い森林の各点に確率 q で木が存在するとき,山火事の拡散をパーコレーションに見立て,ある点に発生した火災が無限の遠方に拡散されるときの臨界確率 qc を議論している.
その他に,自己組織化臨界の性質を持つ森林火災モデルも提案されている.
自己組織化臨界とは相互作用のある大規模な系において,初期状態に依らず,また外部入力無しにある臨界状態に移行していく性質を指す[34].
文献[35-37]では,落雷に起因される森林火災と木の生育がそれぞれある確率で起きるようなモデルを提案し,森林における木の密度がある一定の値に向かう自己組織化臨界の性質を議論している.
木の密度がある臨界密度(臨界状態における密度)より高い状態であれば(過臨界状態),時間発展につれて密度が減少していき,逆に木の密度が臨界密度より低ければ(亜臨界状態),密度が増大するといった挙動が数値的・解析的に示されている.
パーコレーション理論
ここでは,パーコレーション理論に関する研究を紹介する.
パーコレーション理論とは,ある点から始まった水の浸透やある点に発生した病気などが,全域に拡散(伝播)されるかどうかを議論するものである[14].
一般的によく用いられる二次元正方格子のパーコレーションでは,浸透する媒体(森林火災における木や、病気の伝播における人など)が二次元正方格子の各格子に確率 q で存在することを仮定する.
このときある臨界確率 qc を境にして,媒体が全域に浸透する可能性が高いか,もしくは確率1で浸透が途中で収まるかが分かれる.
パーコレーション理論では主にこの臨界確率 qc について議論がなされており,二次元正方格子パーコレーションの臨界確率は[15]によって導出されている.
文献[28]では,パーコレーションと非常に関連性の深いランダムクラスターモデルを扱っている.
ランダムクラスターモデルは,ノード(頂点)とエッジ(枝)からなるグラフを考え,各エッジの状態(openもしくはclosed)をある確率測度に従って与えるモデルである(状態がopenであるエッジを媒体が浸透するという解釈の基で,パーコレーションとの類似性が議論されている[28]).
このモデルは,強磁性体の簡略化モデルとして知られているイジングモデルとの関係も深く,近年広く研究されている.
文献[29,30]では,エッジの状態が時間に対して変化する動的なランダムクラスターモデルを提案している.
文献[32,33]では,正方格子において垂直方向のエッジがopenである確率と水平方向のエッジがopenである確率が異なった非同次パーコレーションを扱っている.
特に[32]では,非同次パーコレーションの臨界確率の厳密解を解析的に導出している.
森林火災モデルの提案 ~複数状態確率セルオートマトン~
森林火災の拡散を表すモデルの一つとして,確率セルオートマトンモデル[46]が提案されている.
確率セルオートマトン[47]とは,正方格子や三角格子などの規則的な格子を考え,各格子の状態が近傍の格子の状態に依存した更新則に従い,確率的に状態遷移するモデルである.
確率セルオートマトンは近傍との複雑な相互作用を有するモデルに広く応用されており,生物膜モデル[42]や格子結晶モデル[43],株市場モデル[44],伝染病モデル[45]などが応用例として挙げられる.
文献[46]で提案されている森林火災の確率セルオートマトンモデルでは,森林を二次元正方格子と捉え,各格子が未燃焼の状態( x=0,x:状態),燃焼状態( x=1 )のどちらかの状態をとると仮定する.
さらに,炎の燃え移りを確率的な事象と捉え、燃焼状態の近傍の格子に確率 p で燃え移ると仮定することで,少ないパラメータで炎の拡散を表現することができる.
ところで,通常の確率セルオートマトンは2つの状態のみを扱うため,現実の複雑な現象とは異なった挙動を示す場合が多い.
この欠点を補完するため,いくつかの論文では状態数を複数に拡張した確率セルオートマトンの応用モデルを提案している[38,39].
文献[40]では,車両の台数を状態と対応させた道路における車両の流れの確率セルオートマトンモデルを提案している.
また文献[41]では,市場における顧客の商品購買モデルを,複数存在する商品群の各商品を状態と対応させた確率セルオートマトンとして表現している.
森林火災の場合,従来の確率セルオートマトンモデルでは2値化された状態表現により火の強弱を表せない.
しかし実際の森林火災においては火の強弱が存在し,燃焼の状態によって近傍に燃え移る確率も変動する.
そこで本研究では,炎の強弱に対応した複数の状態を導入し,先行研究による提案モデルとは異なる新たな複数状態確率セルオートマトンモデルを提案する.
すなわち,未燃焼の状態( x=0 ),燃え尽きた状態( x=n )に加え,n-1通りの燃焼状態( x=1,…,n-1 )を考える.
また,状態 i のセルからその近傍に燃え移る確率(伝播確率)を pi とし,伝播確率が燃焼状態に依存する仕組みを与える.
さらに,燃焼状態にあるセルは与えられた遷移速度行列 A に従って確率的に遷移することとする.
このように複数の燃焼状態を考えることよって,従来のモデルに比べより現実に則した森林火災拡散モデルを提案する.
補足として,本研究で扱う複数状態確率セルオートマトンは,伝染病の蔓延モデル等といった伝播物拡散モデルにも適用可能であると考えられる.

複数状態確率セルオートマトンの解析 ~拡散臨界面~
火災による森林の被害の減少を目的とし,消火ビークルの制御則を考える場合,パーコレーション理論で扱われる臨界確率は消火の一つの指標として用いることができると予想される.
そこで本研究では,パーコレーション理論での臨界確率に対応する,複数状態確率セルオートマトンの拡散臨界面を導出することを目指す.
従来の研究では,Domany-Kinzelモデルと呼ばれる一次元の特殊なセルオートマトンモデルを二次元の有向パーコレーションモデルに変換し,臨界確率の上界値,下界値を解析的に求めている[26,27].
文献[16-19]では,森林火災や病気の伝播等に代表される時間を含むダイナミックな二次元のモデルを,二次元の空間に時間軸を加えた三次元有向パーコレーションに変換し,臨界確率を導出している.
しかし,三次元有向パーコレーションの臨界確率を厳密に求めることは困難であり,また本研究で提案する複数状態の確率セルオートマトンには適用できない.
そこで本研究では,2つの手法を用いて拡散臨界面を導出する.
第一に,確率セルオートマトンの平均場近似[20-22]を拡張し,提案モデルに対する二次元正方格子全域の各状態の割合に関するダイナミクスを導出する.
そして求めたダイナミクスの定常状態から,既に近似解が求まっている二次元正方格子のサイトパーコレーションの臨界確率の値( pc=0.592746 )を用いて,提案モデルの拡散臨界面を求める.
第二に,複数状態確率セルオートマトンを3状態の確率セルオートマトンと関連付け,ボンドパーコレーション理論を応用した3状態確率セルオートマトンの拡散臨界面[48]を用いることで,複数状態確率セルオートマトンの拡散臨界面を導出する.
平均場近似を用いた拡散臨界面の導出
確率セルオートマトンの平均場近似とは,各セルの状態推移を個別に考えずに,格子全体の平均的な状態推移のダイナミクスを近似的に導出する手法である.
本研究では平均場近似を用いて,時間に対する各状態の割合のダイナミクスを導出する.
つまり,ある時刻における状態 x=i のセルの全体の割合を yi とし,y1 から yn の近似ダイナミクスを導く.
このとき本研究で提案するモデルの拡散臨界面は,燃え尽きたセルの割合( yn )の定常状態の値がサイトパーコレーションの臨界確率値(0.592746)より大きくなるような pi の下限値と近似することが出来る.
さらに,yn の定常状態の値は解析的に解くことが出来る.
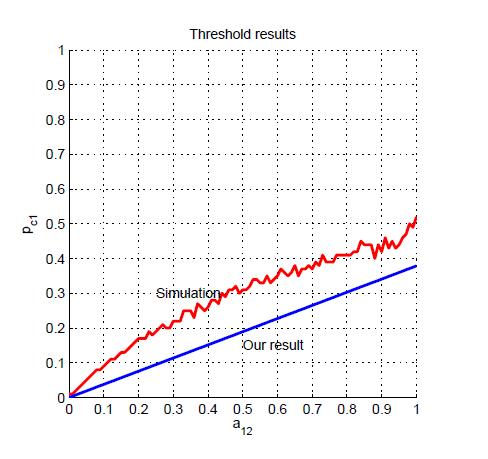
下図に,状態が3つのケースにおいて平均場近似を用いて解析的に導出した拡散臨界面(青線)と,シミュレーションで得られた拡散臨界面(赤線)を示す.
ここで,縦軸は状態1の伝播確率 p1 であり,横軸は遷移速度行列 A の要素 a12 の値である.
またシミュレーションでは,100×100の格子を用いて,中心に点火した炎が格子の境界まで到達するような pi の下限を拡散臨界面として導出している.
遷移率条件を付加した場合の拡散臨界面の厳密解導出
ここでは,遷移速度行列 A に条件を付加した特別なケースにおける拡散臨界面を導出する.
いま,燃えているセルの状態( x=i )が,正の方向にのみ状態遷移( x=j,j>i )するケースを考える.
つまり,遷移速度行列 A の負の方向への状態遷移確率を表す要素が0であるという条件を付加する.
このとき,各状態は多くとも一度しか通らないという特性を活かすことで, n 状態確率セルオートマトンを既存の3状態確率セルオートマトンに変換することが出来る.
さらに,ボンドパーコレーション理論で知られる臨界確率値(0.5)を応用することで,3状態確率セルオートマトンの拡散臨界面の厳密解が得られる[48].
よって,元の複数状態確率セルオートマトンの拡散臨界面が厳密に導出されることになる.
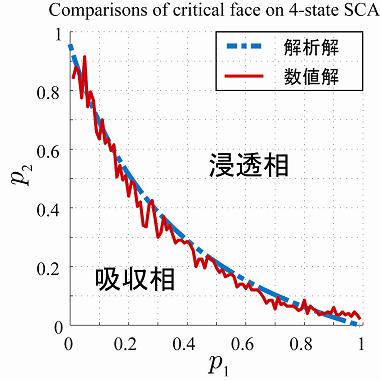
下図に,状態数が4のケースにおける拡散臨界面の解析解(青線),シミュレーションで得られた数値解(赤線)を示す.
ここで,横軸は状態1の伝播確率 p1 ,縦軸は状態2の伝播確率 p2 を表している.
またシミュレーションでは,100×100の格子を用いて,中心に点火した炎が格子の境界まで到達する p1 と p2 の下限を臨界確率として導出している.
上記の結果は,遷移率に関する条件を取り除いた場合にも拡張することが出来る.
状態が負の方向に遷移する状況においても,同じ状態を無限個複製することで,状態が正の方向のみ遷移する状況を作り出すことができ,遷移率条件を付加した場合と同様に既存の3状態確率セルオートマトンに変換することで,拡散臨界面の厳密解が導かれる.
複数状態確率セルオートマトンの拡散阻止制御
森林火災においては,特定の木やエリアの消火を通して火災の拡散を阻止することが要求される.
また,伝染病においては,ワクチンや感染者隔離等を行いウィルスの蔓延を阻止することが要求されている.
このように,伝播物拡散モデルにおいては,近傍への伝播を抑止する制御を特定のセルに加えることで,伝播物の拡散を阻止する制御が求められている.
そこで本研究では,制御入力を加えた複数状態確率セルオートマトンを定式化し,拡散阻止制御手法を提案する.
セルの状態の遷移率を強制的に変化させ,伝播の抑制を誘発する入力を制御入力とし,所与の入力間隔毎に選択された特定のセルに制御入力を加えることを考える.
さらに,複数状態確率セルオートマトンの解析として導出した拡散臨界面を用いることで,森林火災において確率1で有限時間内に全ての炎が消失することを保証する制御手法を提案した.
提案した手法を用いた制御による,拡散阻止の様子を下図に示す.
ここで,水色で示されているセルが制御入力が加わっているセルに対応する.
制御が加わっていない時には火災が遠方に拡散される傾向が見て取れるが,制御を加えることで火災の拡散が有限の範囲に留まる.

参考文献
[1] 林野庁HP(http://www.rinya.maff.go.jp/)
[2] E. Paster, L. Zarate, E. Planas, and J. Arnaldos, "Mathematical models and calculation systems for the study of wildland fire behaviour,'' Progress in Energy and Combustion Science, vol. 29, pp. 139-153, 2003.
[3] A. L. Sullivan, "A review of wildland fire spread modelling, 1990-present 3: Mathematical analogues and simulation models,'' Int. J. Wildland Fire, 2008.
[4] M. A. Finney, "FARSITE: Fire area simulator--model development and evaluation,'' Res. Pap. RMRS-RP-4, 2004.
[5] J. Glasa and L. Halada, "On elliptical model for forest fire spread modeling and simulation,'' Math. Comp. Sim., vol. 78, pp. 76-88, 2008.
[6] S. D. Watt, A. J. Roberts, and R. O. Weber, "Dimensional reduction of a bushfire model,'' Math. Comp. Mod., vol. 21, pp. 79-83, 1995.
[7] V. Mendez and J. E. Llebot, "Hyperbolic reaction-diffusion equations for a forest fire model,'' Phys. Rev. E, vol. 56, pp. 6557-6563, 1997.
[8] I. Karafyllidis and A. Thanailakis, "A model for predicting forest fire spreading using cellular automata,'' Ecological Modelling, vol. 99, pp. 87-97, 1997.
[9] I. Karafyllidis, "Design of a dedicated parallel processor for the prediction of forest fire spreading using cellular automata and genetic algorithms,'' Engineering Applications of Artificial Intelligence, vol. 17, pp. 19-36, 2004.
[10] A. H. Encinas, L. H. Encinas, S. H. White, A. M. Rey, and G. R. Sanchez, "Simulation of forest fire fronts using cellular automata,'' Adv. Eng. Sof., vol. 38, pp. 372-378, 2007
[11] L. H. Encinas, S. H. White, A. M. Rey, and G. R. Sanchez, "Modelling forest fire spread using hexagonal cellular automata,'' App. Math. Mod., vol. 31, pp. 1213-1227, 2007.
[12] B. Porterie, N. Zekri, J. P. Clerc, and J. C. Loraud, "Modeling forest fire spread and spotting process with small world networks, '' Combustion and Flame, vol. 149, pp. 63-78, 2007.
[13] W. Niessen and A. Blumen, "Dynamics of forest fires as a directed percolation model,'' J. Phys. A: Math. Gen., vol. 19, pp. L289-L293, 1986.
[14] D. Stauffer and A. Aharony, Introduction to Percolation Theory, CRC Press, 1994.
[15] H. Kesten, "The critical probability of bond percolation on the square lattice equals 1/2,'' Commu. Math. Phys., vol. 74, pp. 41-59, 1980.
[16] S. R. Broadbent and J. M. Hammersley, "Percolation processes. I. Crystals and mazes,'' Proc. Camb. Philos. Soc., vol. 53, pp. 629-641, 1957.
[17] B. P. Lee, "Renormalization group calculation for the reaction kA + 0,'' J. Phys. A, vol. 27, pp. 2633-2652, 1994.
[18] H. K. Janssen, "Renormalized field theory of dynamical percolation,'' Z. Phys. B, vol. 58, pp. 311-317, 1985.
[19] C. Bezuidenhout and G. Grimmett, "The critical contact process dies out,'' Ann. Prob., vol. 18, pp. 1462-1482, 1990.
[20] J. van den Berg, G. Grimmett, and R. Schinazi, "Dependent random graphs and spatial epidemics,'' Ann. App. Prob., vol. 8, pp. 317-336, 1998.
[21] A. Messer and H. Hinrichsen, "Crossover from directed percolation to mean field behavior in the diffusive contact process,'' J. Stat. Mech., P04024, 2008.
[22] J. A. Filipe and G. J. Gibson, "Studying and approximating spatio-temporal models for epidemic spread and control,'' Phil. Trans. R. Soc. Lond. B, vol. 353, pp. 2153-2162, 1998.
[23] H. K. Janssen, "Logarithmic corrections in dynamic isotropic percolation,'' Phys. Rev. E, vol. 68, 036131.1-036131.9, 2003.
[24] H. K. Janssen and U. Tauber, "The field theory approach to percolation process,'' Ann. Phys., vol. 315, pp. 147-192, 2005.
[25] P. J. Riggan, J. W. Hoffman, and J. A. Brass, "Estimating fire properties by remote sensing,'' IEEE A&E Sys. Mag., vol. 24, pp. 13-19, 2009.
[26] E. Domany and W. Kinzel, "Equivalence of cellular automata to Ising models and directed percolation,'' Phys. Rev. Let., vol. 53, pp. 311-314, 1984.
[27] Makoto Katori and Hiroshi Tsukahara, "Two-neighbour stochastic cellular automata and their planar lattice duals,'' J. Phys. A, vol. 28, pp. 3935-3957, 1995.
[28] G. Grimmett, The Random-Cluster Model, Springer, 2006.
[29] J. Wang, "Sweeny and Gliozzi dynamics for simulations of Potts models in the Fortuin-Kasteleyn representation,'' Phys. Rev. E, vol. 66, pp. 057101.1-057101.4, 2002.
[30] Y. Deng, T. Garoni, and A. Sokal, "Critical speeding-up in the local dynamics of the random-cluster model,'' Phys. Rev. Let., vol. 98, pp. 230602.1-230602.4, 2007.
[31] M. J. Kearney, "Compact directed percolation with modified boundary rules: a forest fire model,'' J. Phys. A: Math. Gen., vol. 35, pp. L421-L425, 2002.
[32] B. Y. Zhang, "A note on inhomogeneous percolation,'' Ann. Prob., vol. 22, pp. 803-819, 1994.
[33] B. Lima and A. Procacci, "A note on anisotropic percolation,'' Let. Math. Phys., vol. 70, pp. 223-229, 2004.
[34] P. Bak, C. Tang, and K. Wiesenfeld, "Self-organized criticality,'' Phys. Rev. A, vol. 38, pp. 364-374, 1988.
[35] B. Drossel and F. Schwabl, "Self-organized critical forest-fire model,'' Phys. Rev. Let., vol. 69, pp. 1629-1632, 1992.
[36] C. L. Henley, "Statics of a self-organized percolation model,'' Phys. Rev. Let., vol. 71, pp. 2741-2744, 1993.
[37] K. Schenk, B. Drossel, S. Clar, and F. Schwabl, "Finite-size effects in the self-organized critical forest-fire model,'' Eur. Phys. J. B, vol. 15, pp. 177-185, 2000.
[38] S. Bandini and G. Pavesi, "Controlled generation of two-dimensional patterns based on stochastic cellular automata,'' Fut. Gen. Comp. Sys., vol. 18, pp. 973-981, 2002.
[39] B. S. Soares-Filho, G. C. Cerqueira, and C. L. Pennachin, "DINAMICA--a stochastic cellular automata model designed to simulate the landscape dynamics in an Amazonian colonization frontier,'' Eco. Mod., vol. 154, pp. 217-235, 2002.
[40] R. Jiang, B. Jia, and Q. Wu, "Stochastic multi-value cellular automata models for bicycle flow,'' J. Phys. A: Math. Gen., vol. 37, pp. 2063-2072, 2004.
[41] J. F. Rouhaud, "Cellular automata and consumer behaviour,'' Eur. Jour. Eco. Soc. Sys., vol. 14, pp. 37-52, 2000.
[42] S. Mourachov and V. P. Poliakov, "Analysis of diamond crystal growth stability from graphite through a film of the metal solvent,'' Diam. Rel. Mat., vol. 7, pp. 309-312, 1998.
[43] G. Pizarro, D. Griffeath, and D. R. Noguera, "Quantitative cellular automaton model for biofilms,'' J. Env. Eng., vol. 127, pp. 782-789, 2001.
[44] M. Bartolozzi and A. W. Thomas, "Stochastic cellular automata model for stock market dynamics,'' Phys. Rev. E, vol. 69, 2004.
[45] L. Monteiro, H. Cimara, and J. Berlinck, "Big cities: shelters for contagious diseases,'' Eco. Mod., vol. 197, pp. 258-262, 2006.
[46] A. Dobnikar, S. Vavpotic, and A. Likar, "Dynamic systems modeling with stochastic cellular automata,'' J. Comp. Inf. Tech., vol. 10, pp. 251-259, 2002.
[47] W. Kinzel, "Phase transitions of cellular automata,'' Z. Phys. B, vol. 58, pp. 229-244, 1985.
[48] K. Kuulasmaa, "The spatial general epidemic and locally dependent random graphs,'' J. Appl. Prob., vol. 19, pp. 745-758, 1982.