Formation Flying Control of Coplanar Spacecraft in Elliptical Reference Orbit

Le Tin Duc

2009 Oct 30

Background

In the general case where the reference orbit is elliptical, several models have concentrated on using the analytical solution of state transition matrix (STM) and the condition of maintaining the same period between followers. In [1], time-explicit representation of STM was derived with approximation to the second order of eccentricity. The approximation removes the singularity of the STM as well as guarantees a very high accuracy compared to the first-order approximation though the drawback is to cope with a complex equations of motion. On the contrary to time-explicit representation of reference orbit with moderate eccentricity, the true anomaly of a leader is prefered to be taken as a time variable. Tschauner-Hempel (TH) equations [2] represents a model which normalizes relative position to time-varying reference radius. Inahal et al. [3] provided the conditions necessary to initialize a closed-form on eccentric orbit which guarantees the leader and the follower have the same period. The conditions are also equivalent by using orbital energy matching approach. Recently, Sengupta et al. [4] presented a parameterization for formation geometry using TH model as a basis. The research in [5] contributes to an explanation of geometry and spatial characters of the relative orbit by approximating the first-order relative position equations algebraically. The paper also reveals that relative orbit always rests on one of the three types of quadratic surfaces (hyperboloid, elliptic cone, elliptic cylinder). In [9], the formation control problem is inspired by cyclic pursuit laws in the ring topology but developed in three dimensions.

Many formation control approaches have been proposed to design relative motion orbits. To match the periodity of spacecraft with minimal fuel cost, linear programming problem is formulated in [3]. In [6], the optimization solution of time and fuel using the Hamilton-Jacobi-Bellman model is developed using spline approximation to evaluate thrust effect. Using the Gauss's Variational Equations (GVE), the control law in [7] aimed to optimize the discontinuous firing fuel. The control approach in [8] made use of Broucke's equations offering the design of spacecraft configuration to achieve mission requiremets, such as vehicle seperation at perigee/apogee or minimum seperation. The control law in cyclic pursuit-inspired formation [9] is considered the feedback control of the relative position with respect to the positions of two agents nearby. The spacecraft converge to a variety of formations, including circular formations and evenly spaced Archimedes' spirals, depending on the parameter of the feedback matrix. Some controllers, including feedforward error dynamics, feedback linearisation with PD control, integrator backstepping, are introduced in [10]. The feasilbility seems to be limited since the control input is associated with the disturbance force which is undeterminable. Research in [11] aimed to take into account of Earth oblateness in design of rotating symmetric grid formations in Low Earth Orbit. The dynamics was approximated under J₂ and J₃ terms. The radius of the formation is time-varying with the formation shape unchanged.

Research Abstract

Our previous research utilized the artificial potential field applied to N coplanar followers in order to drive the followers to a desired equiangular formation with the uncontrolled leader in the orgin of the relative coordinate. With the proposed transformation from rotational Hill's coordinates to new translational coordinates, it is obvious that to achieve the followers' free orbit, there is no need to consider a reference convergence point.

At the attempt to apply the control method of previous work to the formation with elliptical leader orbit, the follower orbits do not appear to be the Keplerian orbits. The next attempt is to clarify the behavior of the orbits mentioned above.

This research extends the previous work by considering the leader in an elliptical orbit. If the leader and the follower has the same Keplerian orbit whose major axes are inclined with small angle and the same initial true anomaly, then in Hill's coordinates, the follower moves on a straight line (Figure 4). This characteristic can be utilized to design an unchangle angle of view which the leader is the vertex of the angle and each follower locates on each side of the angle.

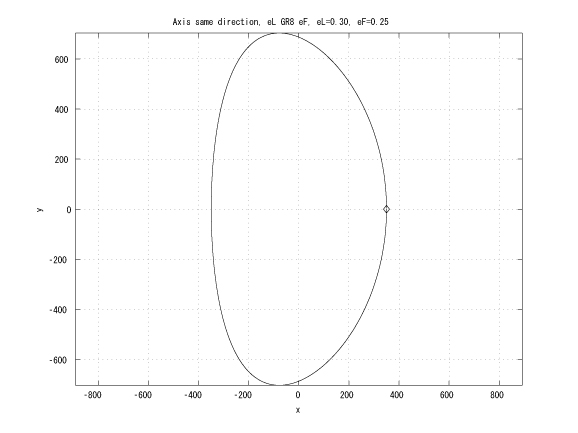
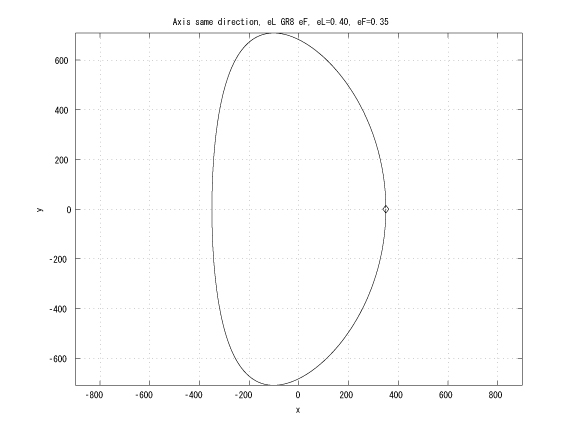
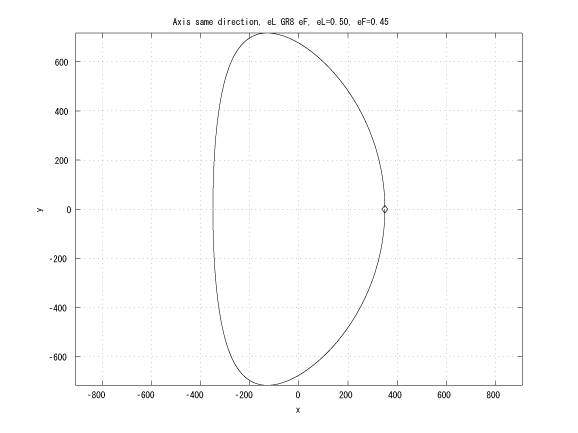
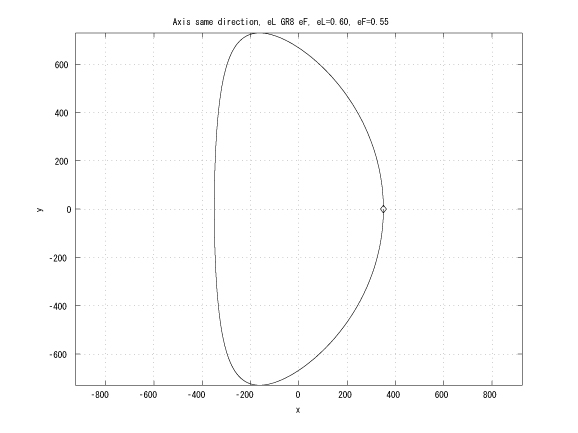
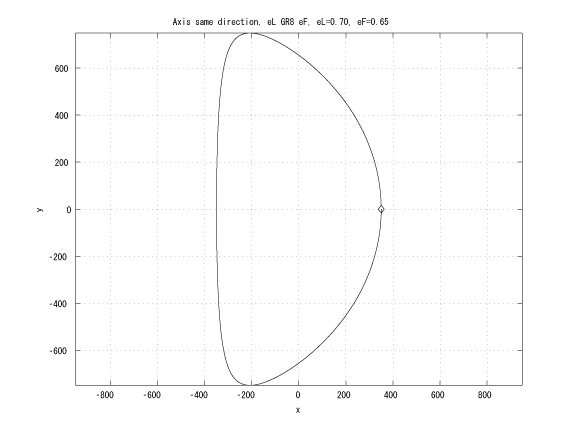
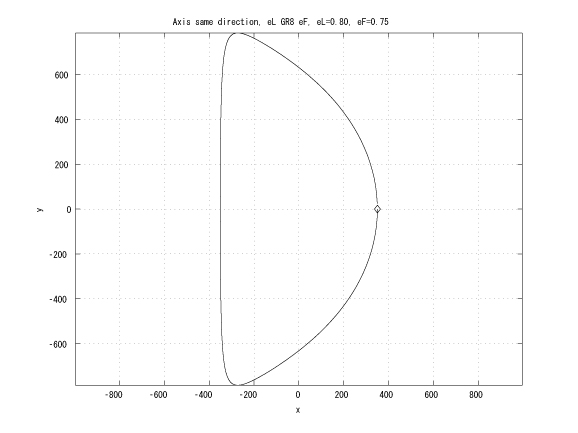
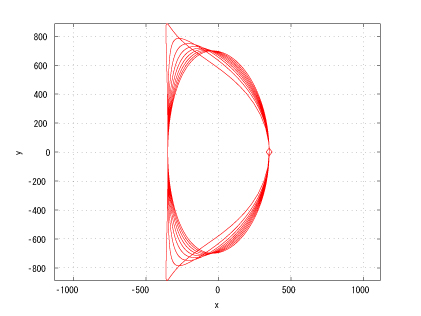
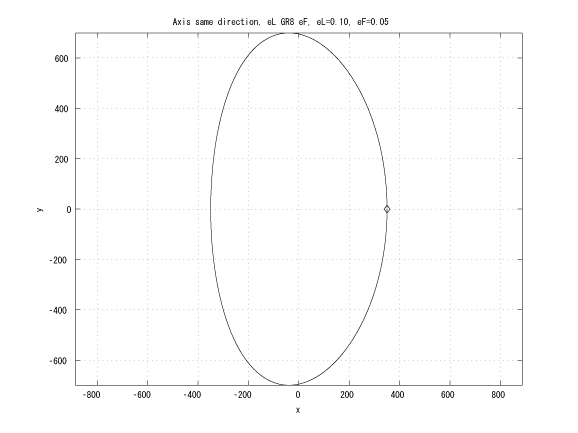
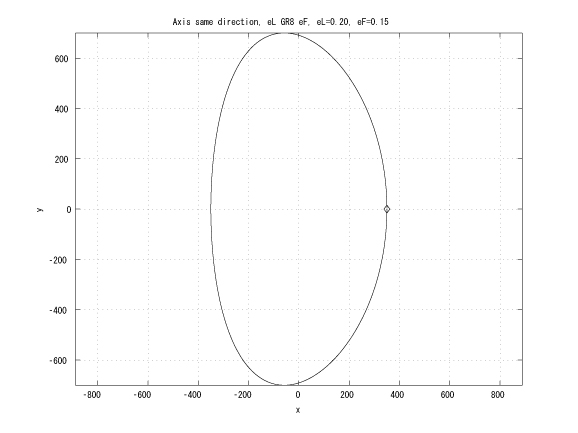
Figure 1: Coaxial major axes, identical initinial true anomalies, e_L > e_F

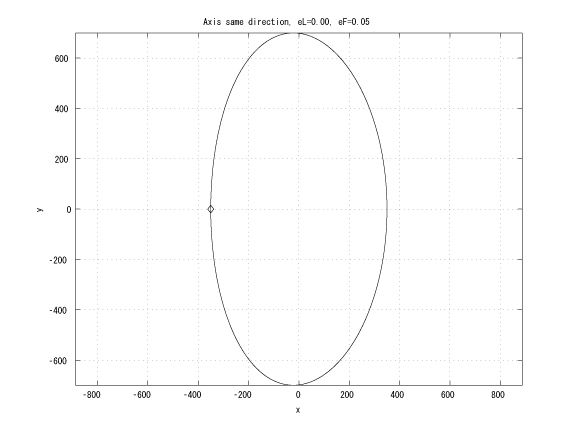
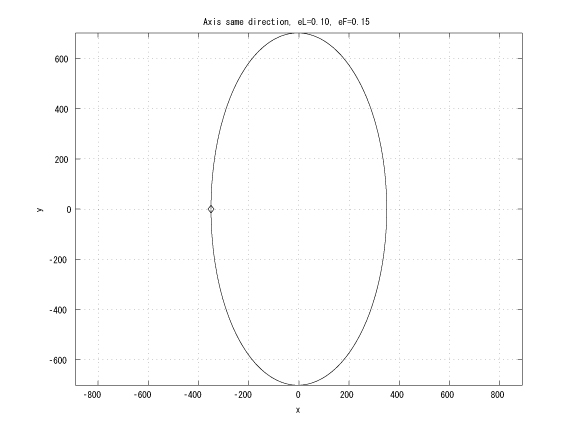
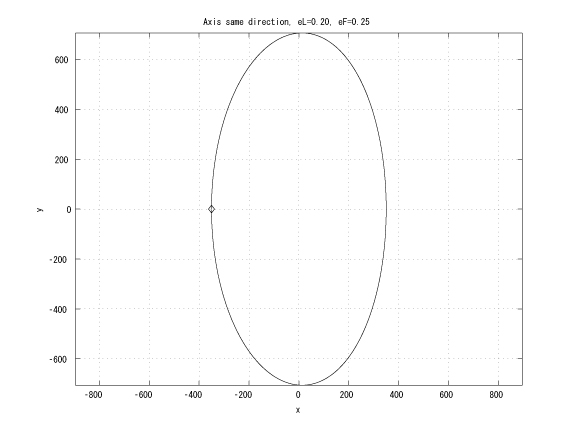
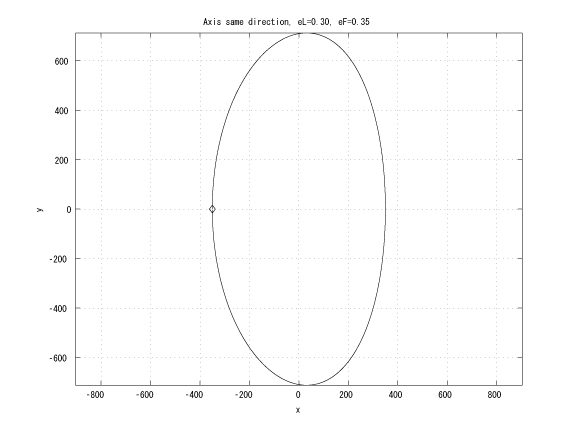
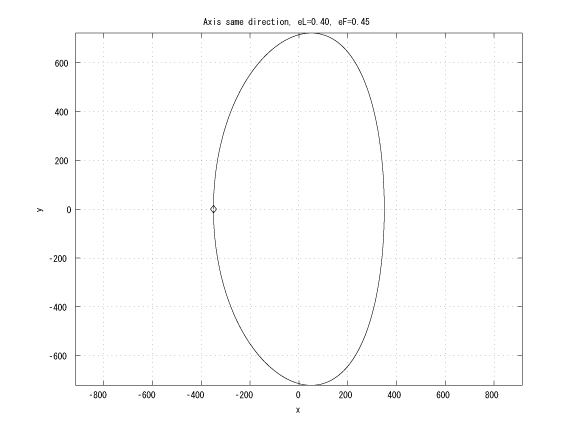
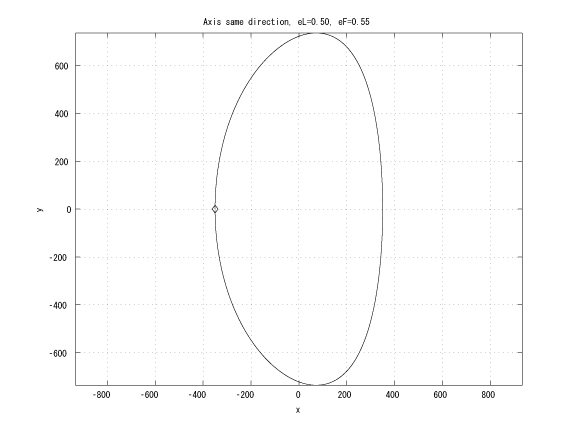
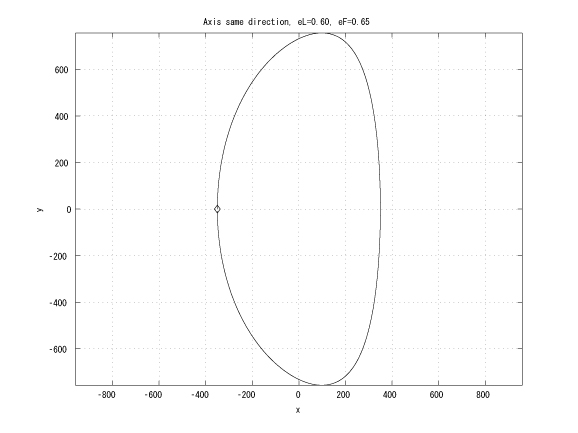
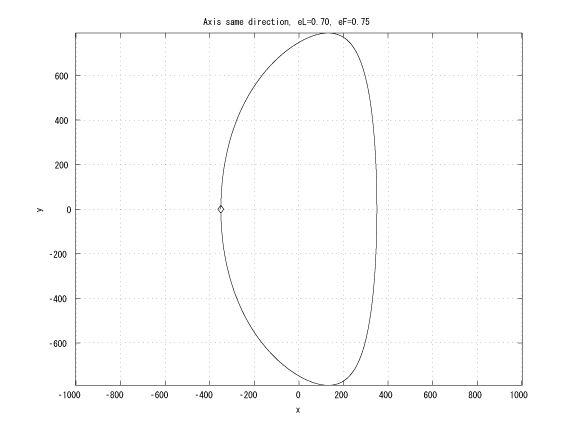
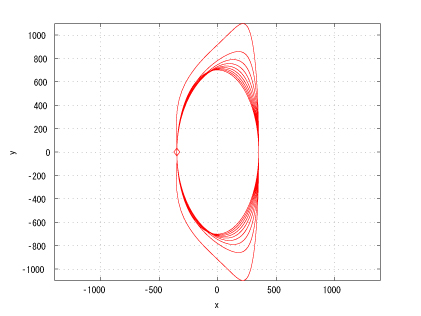
Figure 2: Coaxial major axes, identical initinial true anomalies, e_L < e_F

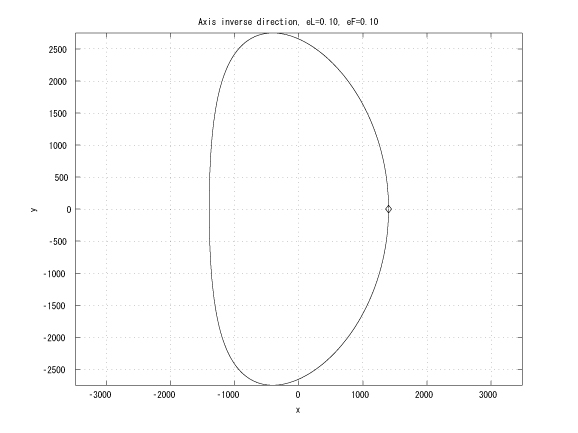
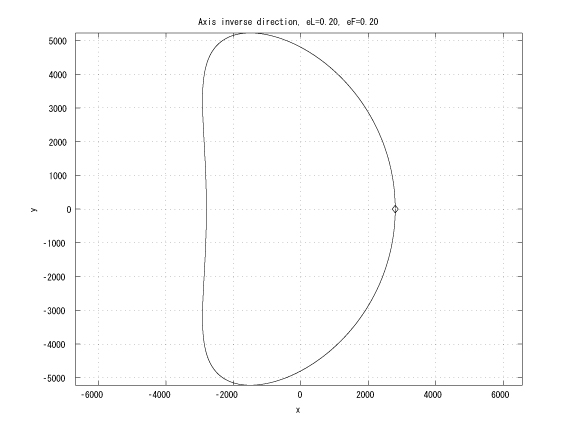
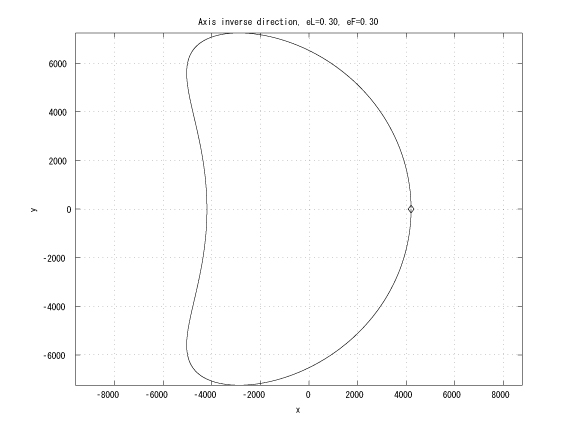
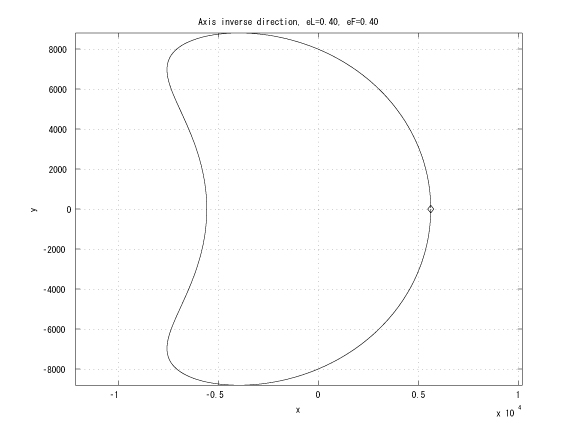
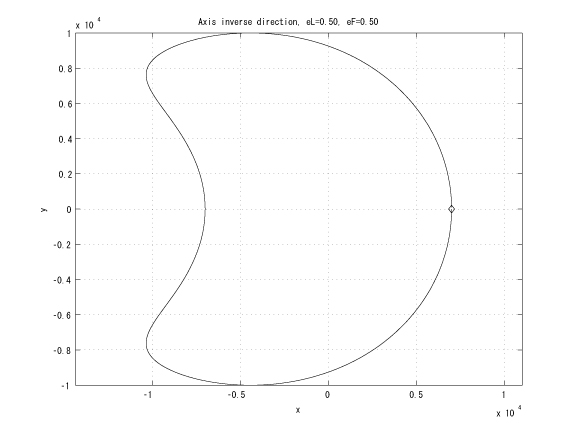
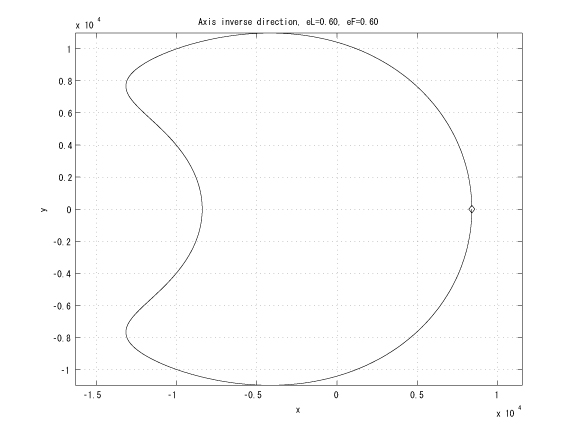
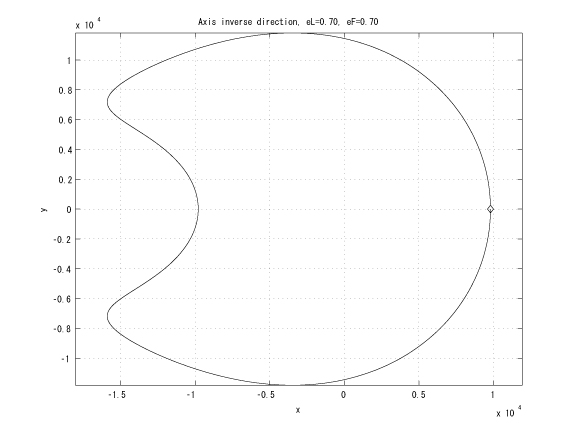
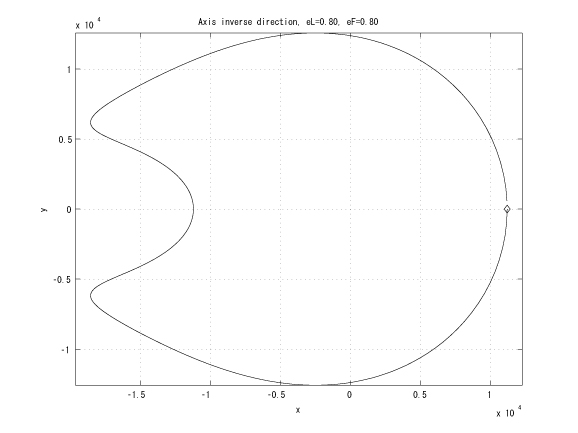
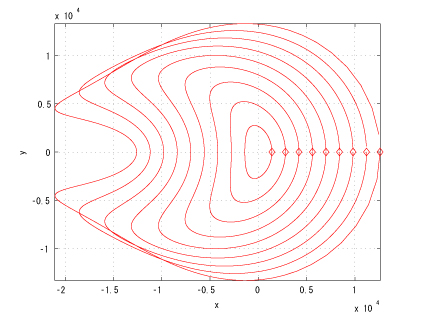
Figure 3: Inverse major axes, initial true anomalies: &theta_L=0 and &theta_F=&pi , e_L = e_F

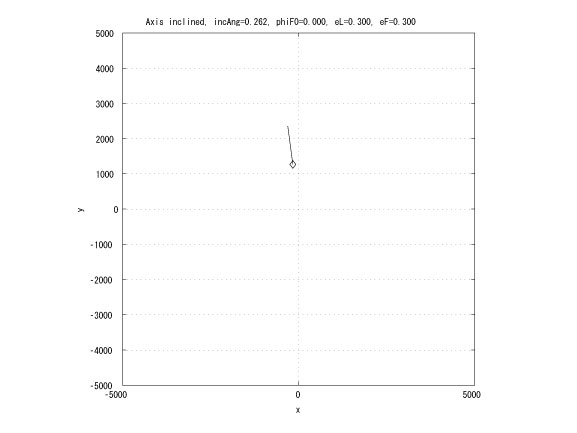
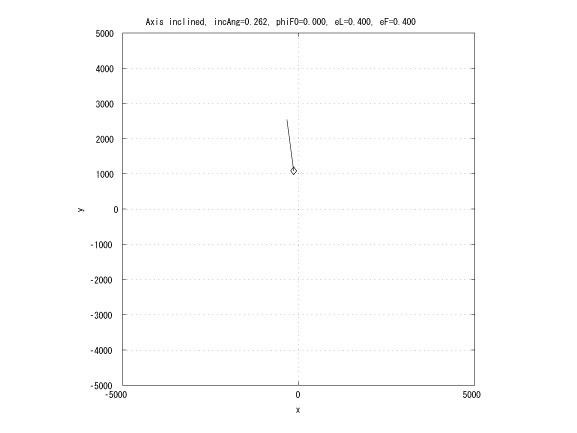
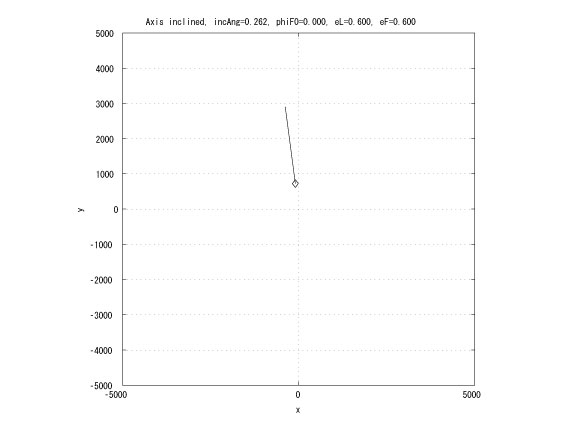
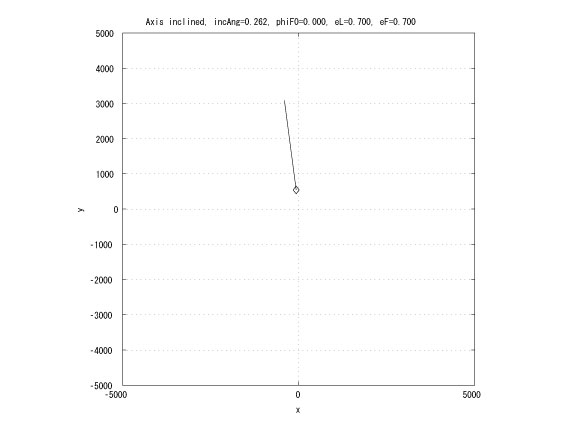
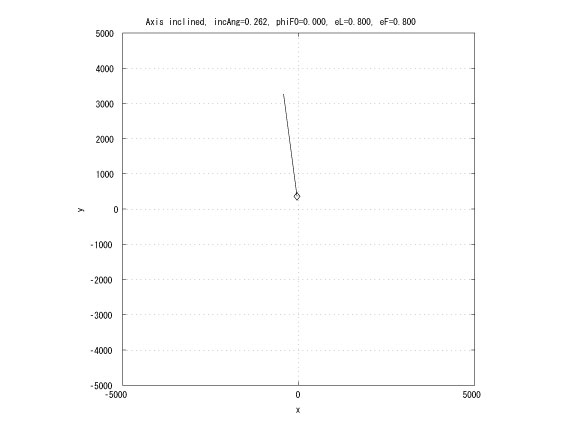
Figure 4: Inclined major axes and equal true anomalies

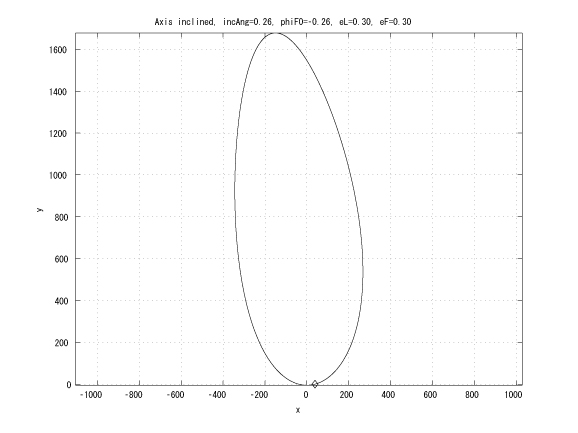
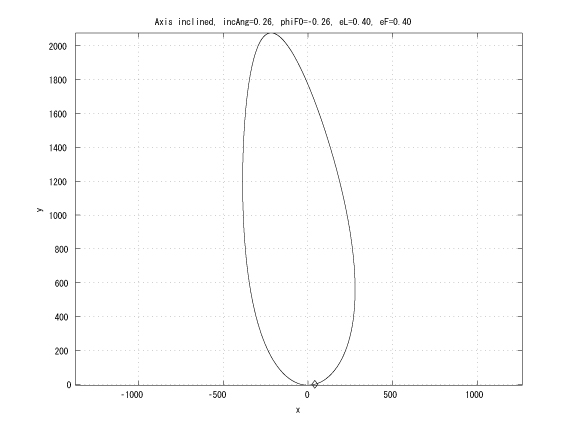
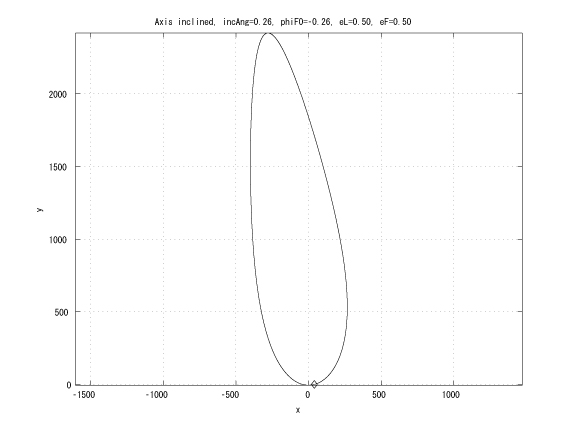
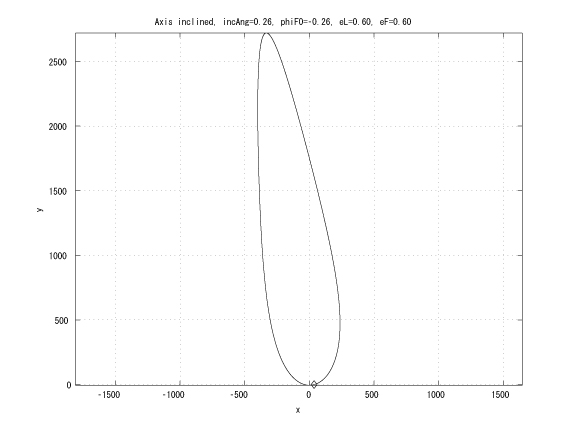
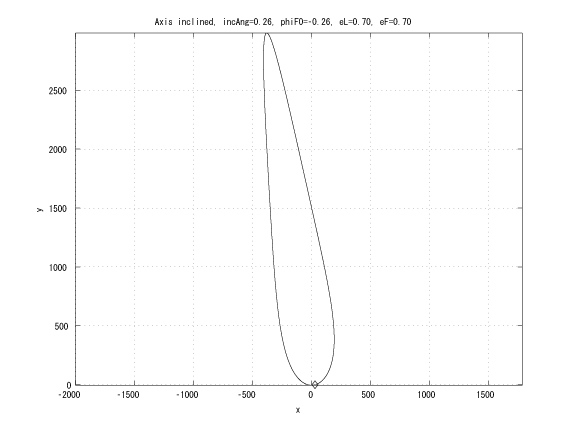
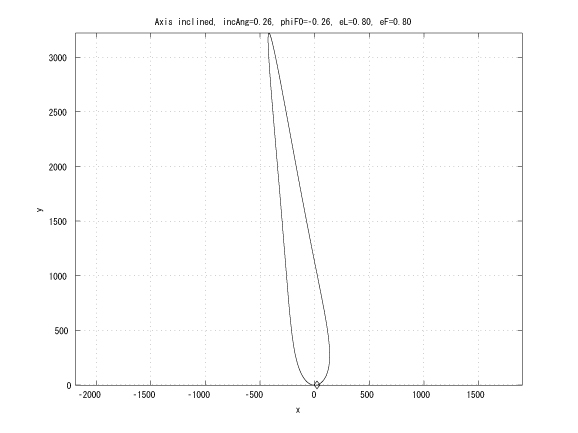
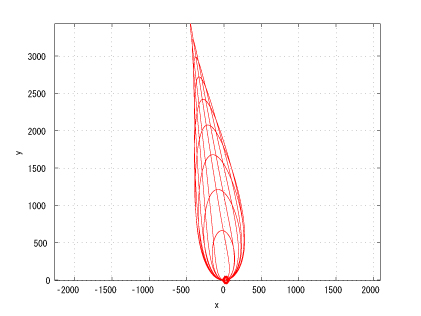
Figure 5: incAng=180⁰/12, folower initial true anomaly, e_L = e_F

------------------------------
References

[1] R. G. Melton, "Time-explicit representation of relative motion between elliptical orbits," AIAA J. Guid. Contr. Dyn, vol. 23, no. 4, pp. 604-610, 2000.

[2] H. Schaub and J. L. Junkins, Analytical Mechanics of Aerospace Systems. AIAA publisher, 2003.

[3] G. Inalhan, M. Tillerson, and J. P. How, "Relative dynamics and control of spacecraft formation in eccentric orbits," AIAA J. Guid. Contr. Dyn, vol. 25, no. 1, pp. 48-59, 2002.

[4] P. Sengupta and S. R. Vadali, "Relative motion and the geometry of formations in keplerian elliptic orbits with arbitrary eccentricity," AIAA J. Guid. Contr. Dyn, vol. 30, no.4, pp. 953-964, 2007.

[5] F. Jiang, J. Li, H. Baoyin, and Y. Gao, "Study on relative orbit geometry of spacecraft formations in elliptical reference orbits," AIAA J. Guid. Contr. Dyn, vol. 31, no. 1, pp. 123-134, 2008.

[6] D. J. Zanon and M. E. Campbell, "Optimal planner for spacecraft formations in elliptical orbits," AIAA J. Guid. Contr. Dyn, vol. 29, no. 1, pp. 161-171, 2006.

[7] L. Breger and J. P. How, "Gauss's variational equation-based dynamics and control for formation flynig spacecraft," AIAA J. Guid. Contr. Dyn, vol. 30, no. 2, pp. 437-448, 2007.

[8] C. Lane and P. Axelrad, "Formation design in eccentric orbits using linearized equations of relative motion," AIAA J. Guid. Contr. Dyn, vol. 29, no. 1, pp. 146-160, 2006.

[9] J. L. Ramirez, M. Pavone, E. Frazzoli, and D. W. Miller, "Distributed control of spacecraft formation via cyclic pursuit: theory and experiments," in Proc. Amer. Contr. Conf., (St. Louis, MO), pp. 4811-4817, June 2009.

[10] R. Kristiansen and P. J. Nicklasson, "Spacecraft formation flying: a review and new results on state feedback control," Acta Astronautica, vol. 65, no. 11-12, pp. 1537-1552, 2009.

[11] P. Palmer and M. Halsall, "Designing natural formations of low-earth-orbiting satellites," AIAA J. Guid. Contr. Dyn, vol. 32, no. 3, pp. 860-868, 2009.