西山 聡史
1. 区分的線形システム
連続時間のダイナミクスとそれを切り替える離散的なダイナミクスとが一体となっているシステムを一般的にハイブリッドシステムと呼ぶ. ハイブリッドシステムはその切り替え要素の種類によって様々な分類がなされているが, その典型的なものの一つに区分的線形システム(Piecewise Linear System)が挙げられる. 区分的線形システムでは状態空間がいくつかの領域に区切られており, 各領域には線形ダイナミクスが割り振られている. Fig.1に区分的線形システムの例を示す. この例では, 上段のばねと接触している状態と, 接触していない状態とで別々の線形ダイナミクスを持つ. 区分的線形システムはハイブリッドシステムの中でもシンプルかつ基本的なものであると言え, これを詳しく解析することはハイブリッド制御理論の確立のために重要な意義を持つ.
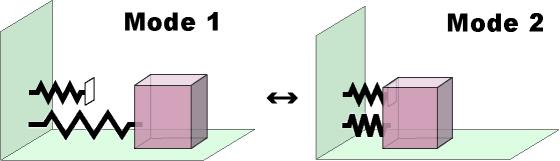
Fig.1 Example of Piecewise Linear System
線形システムは固有値解析によって簡単に安定性を判別できるが, 区分的線形システムの安定性解析はより複雑である. 例えば, 各モードのシステム行列が不安定であってもシステム全体としては安定となるケースも存在する. 区分的線形システムの安定性解析には線形システムとは違った手法が求められる.
2. 区分的線形システム解析理論の背景
昨今の区分的線形システムの研究については[1]が詳しい. 文献[1]では区分的線形システムのモデルの定式化やリアプノフ関数を用いた区分的線形システムの安定性判別手法などについて例を用いて簡潔に説明されている. 文献[2]では区分的線形システムの安定性を考える上での基本的な問題について述べられている.
区分的線形システムを解析するにあたってまず重要な点は, 解析対象であるシステムがwell-posedであるかどうかである. well-posednessとはシステムの解の存在性と一意性のことであり,与えられたハイブリッドシステムがwell-posedであるかどうかを判定する手法については, [3,4]が詳しい. また, 2モード非線形区分的システムのwell-posednessに関しても研究されている[5]. well-posedな平面区分的線形システムの安定性解析については既に幾つかの手法が確立されつつある.
区分的線形システムはその領域の区切り方によって様々な種類のものを考えることができるが, 切り替え面が原点を中心として放射状となっている区分的線形システムは比較的解析が容易であり, 状態変数が2次元の場合に原点が安定であるための必要十分条件が導出されている[6]. また, モード数が2であるような区分的線形システムについては多次元な場合についても[6]が安定性に関する必要条件と十分条件を導出している.
また, 区分的に連続なリアプノフ関数を用いることで安定性を判別する手法も提案されている[7]. この手法は状態変数が多次元, かつ多モードの区分的線形システムにも適用できる利点を持っている. この手法を利用した研究としては[8]などがある. また, [7]の手法では全ての安定な区分的線形システムについてその安定性を判定することはできないが, [9]ではリアプノフ関数を構築する際の区分領域を増やしていくことで安定と判定できる区分的線形システムのクラスを広げる試みが成されている. 以上の研究はすべて連続時間のシステムを取り扱っているが, 離散時間区分的線形システムの安定性に関する研究も行われている[10].
状態変数が3次元以上の区分的線形システムは領域間の遷移が平面時に比べ圧倒的に複雑になるため, その解析は困難となる. 文献[11]では領域間の遷移を明確に定義する"Impact Map"という概念を用いて区分的線形システムの解析に取り組んでいる. また, 同様の手法を応用して区分的線形システムにおけるリミットサイクルの安定性解析[12]や可到達性解析[13]が研究されている. モードの遷移に関する研究としては[14]の区分的線形システムに関するReachable Set問題を取り扱ったものがあり, ハイブリッドオートマタのモード遷移を解析する際のSymbolicな手法について述べている. 安定化手法に関する研究も行われており, [15,16]などがある.
3. 区分的線形システムの切り替え面設計
文献[6]や[7]などで述べられている手法を用いれば, 切り替え面の配置が予め決定されたシステムについて安定性を論じることができる. では, 複数の不安定なシステム行列が与えられたとき, 切り替え面(状態量が2次元の場合は切り替え線)を適切に配置することで, 安定な区分的線形システムを構築することは可能だろうか(Fig. 2).
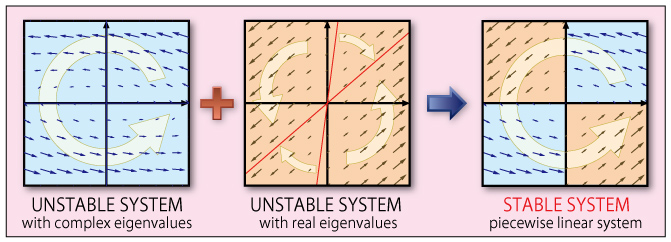
Fig.2 Stable piecewise linear system with unstable subsystems
本研究では, 原点を通る放射状の切り替え線を持つ2次元区分的線形システムについて, 複数の不安定なシステム行列が与えられたとき, 切り替え線を適切に配置し各領域に適切なシステム行列を与えることで安定な区分的線形システムを構築できるか, という問題について考えている. その際, 計算機を用いて逐次的に最適な切り替え線を探索する, という アプローチではなく, 解析的に最適な切り替え線を求めることに主眼を置いて研究を行った.
まず軌跡の回転方向が状態量に依らず同じであるような複素固有値を持つシステム(例:Fig.2左端)を 組み合わせて安定な区分的線形システムを構築する手法を導出し, その後, 実固有値を持つシステム(例:Fig.2中央)へとその手法を拡張した. この手法において, 2次元区分的線形システムを極座標変換したとき, 位相に関するダイナミクスが径のダイナミクスに依らないという事実が鍵となっている. 詳細は文献[17]を参照されたい.
4. 参考文献
| [1] | R. Decarlo, M. Branicky, S. Petersson, and B. Lennartson, ``Perspectives and results on the stability and stabilizability of hybrid systems,'' Proc. IEEE, vol. 88, pp. 1069-1082, 2000. |
| [2] | D. Liberzon and A. S. Morse, ``Basic problems in stability and design of switched systems,'' IEEE Contr. Syst. Mag., vol. 19, no. 5, pp. 59-70, 1999. |
| [3] | J. Imura, ``Well-posedness analysis of switch-driven hybrid systems,'' IEEE Trans. Autom. Contr., vol. 48, no. 11, pp. 1926-1935, 2003. |
| [4] | J. Imura and A. J. van der Schaft, ``Characterization of well-posedness of piecewise linear systems,'' IEEE Trans. Autom. Contr., vol. 45, no. 9, pp. 1600-1619, 2000. |
| [5] | C. Z. Wu, K. L. Teo, and V. Rehbock, ``Well-posedness of bimodal state-based switched systems,'' Appl. Math. Lett., vol. 21, pp. 835-839, 2008. |
| [6] | Y. Iwatani and S. Hara, ``Stability tests and stabilization for piecewise linear systems based on poles and zeros of subsystems,'' Automatica, vol. 10, pp. 1685-1695, 2006. |
| [7] | M. Johansson and A. Rantzer, ``Computation of piecewise quadratic Lyapunov functions for hybrid systems,'' IEEE Trans. Autom. Contr., vol. 43, no. 4, pp. 555-559, 1998. |
| [8] | M. Johansson, ``Piecewise quadratic estimates of domain of attraction for linear systems with saturation,'' in Proc. IFAC World Cong., (Barcelona, Spain), 2002. |
| [9] | J. Oehlerking, H. Burchardt, and O. Theel, ``Fully automated stability verification for piecewise affine systems,'' vol. 4416, pp. 741-745, Springer, 2007. |
| [10] | G. Feng, ``Stability analysis of piecewise discrete-time linear systems,'' IEEE Trans. Autom. Contr., vol. 47, no. 7, pp. 1108-1112, 2002. |
| [11] | J. M. Goncalves, A. Megretski, and A. Dahleh, ``Global analysis of piecewise linear systems using impact maps and surface Lyapnov functions,'' IEEE Trans. Autom. Contr., vol. 48, no. 12, pp. 2089-2106, 2003. |
| [12] | J. M. Goncalves, ``Regions of stability for limit cycle oscillations in piecewise linear systems,'' IEEE Trans. Autom. Contr., vol. 50, no. 11, pp. 1877-1882, 2005. |
| [13] | A. O. Hamadeh and J. M. Goncalves, ``Reachability analysis of continuous-time piecewise linear systems,'' in Proc. Joint IEEE Conf. Dec. Contr. and Eur. Contr. Conf., (Seville, Spain), pp. 4169-4174, 2005. |
| [14] | R. Ghosh and C. Tomlin, ``Symbolic reachable set computation of piecewise affine hybrid automata and its application to biological modelling: Delta-notch protein signalling,'' IEE Sys. Biol., vol. 1, no. 1, pp. 170-183, 2004. |
| [15] | M. A. Wicks, P. Peleties, and R. A. DeCarlo, ``Construction of piecewise Lyapunov functions for stabilizing switched systems,'' Proc. IEEE, vol. 4, pp. 3492-3497, 1994. |
| [16] | M. Johansson, ``On modeling, analysis and design of piecewise linear control systems,'' in Proc. Int. Symp. Circ. Syst., (Bangkok, Thailand), pp. 646-649, 2003. |
| [17] | S. Nishiyama and T. Hayakawa, ``Optimal stable state-space partitioning for piecewise linear planar systems,'' in Proc. Amer. Contr. Conf., (Seattle, WA), pp. 3959-3965, June 2008. |
平成21年4月30日更新