日本では1996年より, 産学官が相互協力して交通事故, 渋滞などの道路交通問題を解決することを目的 とした新しい交通システム(ITS: Intelligent Transport Systems)を構築する体制が整えられている[1]. 「安全運転の支援システム」は 日本のITS事業における開発対象の一つであり, 高速道路における自動車流の制御手法はその関連技術として研究されている. 自動車流の制御が達成されると, 渋滞の解消により物流の効率化や排気ガスの削減が期待できる. また, 渋滞が解消されることに伴う経済効果は年間あたり数十兆円規模と予測されており, 自動車流の制御の研究の意義は大きい.

　高速道路における自動車流の動的モデルは大きく分けて二つに分類される. 一つ目は個々の 自動車の挙動に着目するミクロモデルであり, 二つ目は多数の自動車によって形成される交通 流の挙動に着目するマクロモデルである.

ミクロモデル

　ミクロモデルでは, 個々の自動車の挙動を表現する際に運動方程式を用いる. 車群(vehicle platoon) を形成するとき, 制御目標は二つに大別される. 一つは車間距離を目標値に追従させる 制御則, もう一つは車間時間を目標値に追従させる制御則である. ここで, 車間時間とは, 先行 車両がある地点を通過してから追従車両がその地点を通過するまでの時間のことである. この 二つの制御手法の比較について, [2] に詳しく述べられている. 車群の安定性に関する重要な概 念としてstring stability がある. string stability は, 複数の車両が一列に連なって群走行したと き, 群の前方の車両の速度変化が群の後方の車両に増幅して伝達されないこと, すなわち, 先行 車の位置を入力, 追従車の位置を出力としたときの伝達関数の最大ノルムが１以下になること を保証する. 車間距離を一定に保つ制御方式では, string stability を満たすために, 全ての追従 車両は先頭車両からの相対位置の情報が必要であり車車間通信が要求されるが, 車間時間を一 定に保つ制御方式では, 追従車両は直前の車両の相対位置と速度の情報のみが必要であり, 車車 間通信は要求されない. しかし, 後者の車間時間を一定に保つ制御方式では, 車間時間が短くな ると, それに反比例して大きな入力が必要となるので, 自動車密度が高く, 車間距離が短い場合 には前者の車間距離を一定に保つ制御方式のほうが優れていると結論付けている[2].
　車間時間を目標値に追従させる制御方式については, [3, 4, 5] に詳しく述べられている. 文献 [3] ではstring stability を満たすためには, エンジンの一次遅れ時定数が車間時間の半分を超え てはならないことが述べられている. また, [4] では, 車間時間を一定に保つ制御方式を用いたと きの交通流の安定性を調べている. 多くの論文では, 道路上に自動運転の車両のみが存在する状 況を仮定しているが, [5] では, 自動運転の車両と手動運転の車両が混在する状況で車間時間に 着目した制御手法を考察している.
　一方, 車間距離を目標値に追従させる制御方式については, [6, 7, 8, 9, 10] に詳しく述べら れている. 文献[6] では, 車間距離を目標値に追従させる制御方式において, 目標車間距離を制 動距離としたときにstring stability が成り立つための条件を求めている. 文献[7] では, 目標車 間距離を走行速度の二次関数とし, その二次関数の各係数を制約付き最適化問題の解として求 めている. この目標車間距離に対して, スライディングモード制御の枠組みで入力加速度が導 かれている. 文献[8] では, 前方だけでなく後方の車両との相対位置と相対速度の情報を用いて 制御を行うことを考察している. この際, 前から後ろ方向だけでなく, 後ろから前方向のstring stability をも考慮している. 車両重量や空気抵抗や転がり抵抗を未知パラメータとする場合で も, 車群を安定的に形成する手法を示している文献もある[9]. この文献では, リアプノフベース の適応制御器を用いることで, 車間距離誤差(目標車間距離と実際の車間距離の誤差) が0 の状 態を安定化でき, さらに車間距離誤差をある一定の範囲に収めることができることを示してい る. また, モデル予測制御を用いた車群の形成手法も提案されている[10, 11]. 文献[10] では, 車 間距離誤差, 先行車両と追従車両の相対速度, 入力加速度, 及び入力加速度の時間差分に関する コスト関数を定義し, この関数を最小化するモデル予測制御を行っている.
　ミクロモデルを考察対象とする研究では, 車間距離を目標値に追従させる制御方式を用いる もの, および車間時間を目標値に追従させる制御方式を用いるもののいずれにおいても, 数台か ら数十台程度の車群を形成することに主眼が置かれており数万台規模の高速道路全体の自動車 流の制御にはあまり注意が向けられていない.

マクロモデル

　 　マクロモデルは, 流体力学とのアナロジーで, 高速道路における自動車密度と車両速度によっ て自動車流のダイナミクスを記述する. 文献[4, 12, 13] のモデルでは, 高速道路を数キロ程度 の区間に分割し, 区間ごとに車両速度と自動車密度を定義し, さらにある区間から次の区間へと 単位時間に移動する自動車の台数を定義する. 各区間の車両速度が自動車密度に依存して制御 されているとき, 各区間の自動車密度を並べたものを状態ベクトルとした状態方程式が得られ る. その際, 境界条件の差異によって, 状態方程式で表されるシステムの性質は大きく異なるも のになる. 文献[12] では, 最初の区間に一定の割合で車両が流入し, 最後の区間の状態に依存し て高速道路外へと車両が流出する境界条件を考えている. このとき, 車間時間を一定に保つよう に, 各区間の車両速度を自動車密度に応じて制御すると, システムの平衡点は不安定になること が示されている. 一方, [4] では, 道路の両端がつながっているサーキット状の境界条件を考えて いる. このとき, [12] と同様にして, 車間時間を一定に保つように各区間の車両速度を自動車密 度に応じて制御すると, システムの平衡点は安定になることが示されている. さらに, [13] では 上記の二種類の境界条件の両方を考察対象として, システムの安定性を解析している. 具体的 には, システムの平衡点の安定性を調べるために, 平衡点周りで近似線形化して, 得られたシス テム行列が安定になる条件を調べている. その結果, 自動車密度がある程度低い値であるなら ば, 上記の二種類の境界条件のいずれにおいても, システムの平衡点が安定となることを導いて いる.
　しかし, 自動車密度が高く, 道路が混雑している状況では交通流が不安定になることが示され ており, これは解決しなければならない問題として残されている.

　 　本研究では, マクロモデルにおいて道路全体の交通状況を考慮して安定な交通流を計画し, ミクロモデルにおいて各々の車がこの計画した交通流に従うように各々の車両のアクセルとブレーキを制御することを考える. ただし, 高速道路上の全ての自動車のアクセルとブレーキが自動化されているという 仮定をおく.
　 　まず, 道路全体の交通状況を考慮して安定な交通流を計画するために, [12] の問題設定を拡張し, ある区間の車両速度がその区間の車両密度のみならず次区間の車両密度の関数でもあるとき, システムの平衡点が安定になる条件を調べる. このとき, 車両の速度はより多くの情報を用いて決定されるため, 制御性能が向上することが期待される. また, 先に述べたように, 従来の結果では, 車両密度が高く, 道路が混雑している場合, 平衡点は 不安定になることが示されている. 本研究では, 車両密度が高い場合でも平衡点が安定となるよ うに各区間の車両速度をその区間の車両密度と次区間の車両密度の関数として決定する手法を 考察する.
　次に, 各々の車が上で計画した交通流に従うように速度と車間距離の目標値を与え, この目標値に基づいて個別の車両に対する加速度の入力量を決める.

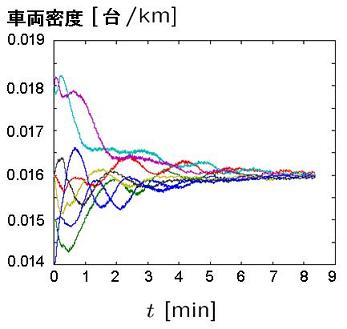
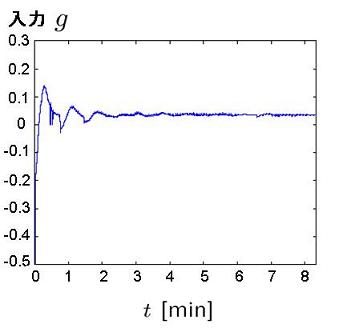
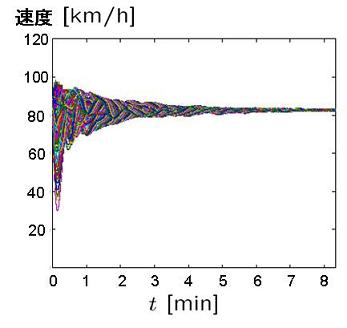
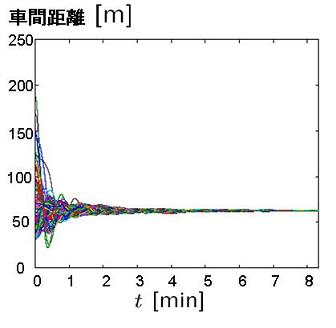
　 　提案した制御方式の性能を検証するために, 数値実験を行った. 一セクションの長さを1 [km], セクション数を8, 車両台数を128 [台], 最高速度100 [km/h] としたときのシミュレーション結果を以下の図1 から図4 に示す. まず図1 より, 車両密度が全ての区間で等しく出来たことがわかる. 次に車両に対する許容加速度入力は0.5g から0.3gと 知られているが, 図2より, この範囲内で入力を収めることが出来たことが確認できる. ただ し, g は重力加速度定数で, g = 9.8 [m/s²] である. さらに図3より, 最高速度を守った上で速 度を一定値に収束させることが出来たことが分かる. 最後に図4 より, 衝突を回避した上で車 間距離を一定値に収束させることが出来たことが確認できる.

図1 車両密度	図2 入力

図3 車両速度	図4 車間距離

　 　まず, 多数の車両によって形成される交通流のマクロモデルに関して先行研究の問題設定を拡張し, 安定性に関する新しい結果を示した. 次に, マクロモデルで計画した交通流を実現するために個別の車両にどのような入力を加えるべきかを考察した. さらに, 数値実験によって, 制御方式の妥当性を検証した.