This research focuses on applying modern control practices to the analysis of delay differential systems, with a specific focus on the application to the congestion control of computer networks. In a typical computer network system, data from one or more computers is sent to one or more other computers through the wires and cables that interconnect the network. If many computers try to send data on the same wire at the same time, that wire may become congested. This is not dissimilar to what happens on a busy highway during rush hour. Figure 1 shows an example of what a typical small network might look like and illustrates how data can move from one computer in the network to another.
It has already been proven in [10] that the current method of maintaining the stability of the Internet as implemented by the TCP protocol is not sustainable and will not be able to handle the increasing speeds of Internet traffic in the future. Consequently there has been a significant amount of research conducted in the past few years (see for example [1,4,7-16]) in an attempt to present a solution to this problem. The specifics of this kind of system also present several unique and non-trivial challenges that must be overcome in order to derive a viable solution.
It is, of course, necessary to define a method by which the network resources can be equally shared between all of the computers wishing to use them. More specifically, if two machines wish to send data along the same wire, they should be able to choose an appropriate rate with which to send data without overflowing the wire and causing congestion. This general statement results in several conditions for the system, namely:

1. the network resources must be shared according to some rule (either equally or unequally)
2. the data rates in the network must eventually converge to a value dictated by rule #1
3. ideally, each computer should be able to adjust its rates without knowing about the rates of the other computers in the network

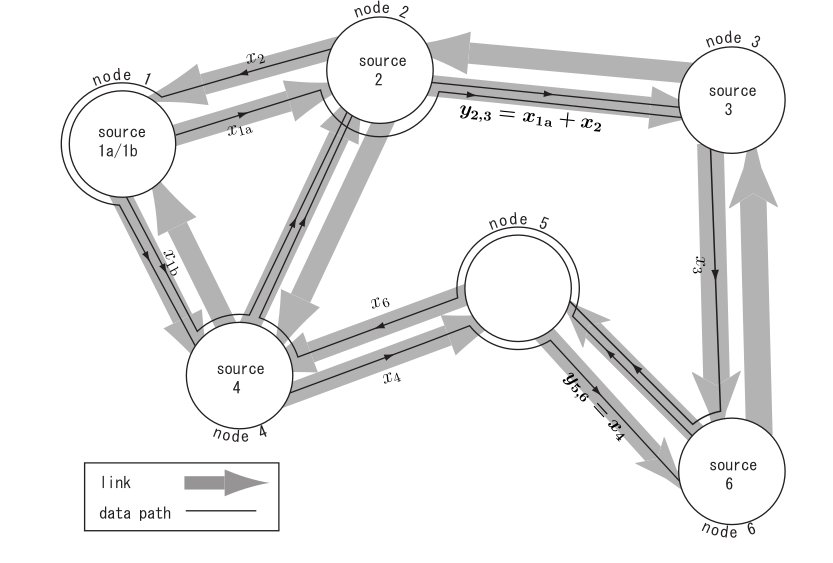
The analysis of this system is further complicated by the presence of delay in the network. As such, the system dynamics are a function not only of the current state, but also of the state at every instant over the previous &tau seconds, where &tau denotes the round-trip time it takes for data to travel from one computer on the network to its destination and for an acknowledgement of that data at the receiver to reach the sender. Consequently, instead of being represented by differential equations, as many systems are, we must represent the system by delay-differential equations, having an infinite dimensional state ([2]). Additionally, with multiple data sources operating in the network, all within different time frames, the analysis of this kind of system quickly becomes extremely difficult.

The control laws presented in [7,9,11,13] do in fact prove the stability of the network under various conditions and assumptions, however they do not attempt to address the depth of the network queues at the steady state. In particular, these control schemes rely on the length of the data queue (as estimated through the round-trip delay time) as an input to the controller. As such, the possibility of requiring a very large steady state queue in order to stabilize the system exists. In this situation, the further possibility that the required queue size for stability will be larger than the physically available queue also exists. Thus, there is a chance that the system cannot be adequately stabilized, possibly resulting in oscillatory behaviour.
In order to address the problem of infinitely growing queues, it is necessary to separate (at least partially) the queue length value from the control input by adding dynamics to the user side data rate calculation, by introducing an additional dimension to the control measurement, or by combining these two methods.
One of the most attractive aspects of the control laws presented in [7,9-11] is the ability of the controller to compensate for the delay inherent in the system, allowing the system to be stabilized regardless of the round-trip time of the data sources in the network. As such, we aim to develop improved control laws that maintain the delay independence of the stability criterion. This is of course not a trivial task, since we must solve a general stability problem, with an arbitrary network analytically, instead of utilizing LMIs or other numerical analysis tools. As a result, adding additional dimensions to the control measurement is far from a straightforward task.
Aside from the complexity of analysis, adding additional feedback poses an additional problem, since the only method to provide additional measurements to the data senders is a serial data interface, wherein a trade-off between response time and data resolution must be made.
The XCP protocol, proposed in [4] uses the serial congestion control interface, namely a single bit in the TCP header, to decouple the queue length value from the control input. This is achieved by adjusting the controller input to include extra dynamics. Adjusting the controller input in this way however, increases the amount of delay in the system, possibly causing it to be slower than if the round-trip-delay measurement were used directly. Despite this, the XCP protocol has many advantages including more fair allocation of network resources, and shorter steady-state queues than the implementations presented in [7,9,11,13].
Unfortunately, the potential advantages of the XCP protocol come at the cost of additional computational overhead at routers and the addition of extra header fields to the existing TCP header. These two aspects combined make implementation of XCP in current networks unlikely. Instead we are investigating a control law with some of the congestion control aspects of XCP using a revised pricing function for the control law presented in [13]. We are currently investigating the stability of a second-order pricing function using numerical methods by taking advantage of the results presented in [5]. This method will combine the round-trip-time measurement with the serial interface to simultaneously maintain stability of the network while controlling the queue length.

In order to implement pricing functions on the serial congestion control interface at the links it is necessary to have a sufficient quantization algorithm. In order to achieve this we must set bounds on the transmitted data values and choose an appropriate quantization method. Since we want to transmit an unbounded link price using this method, it is not immediately clear how to achieve this objective. Fortunately the price we wish to transmit is the result of integrating a bounded quantity (the difference between the current queue level and the desired queue level) and so we can quantize and transmit this bounded quantity from the links and perform the integration over time at the sources.
As stated previously, a trade off between response speed and data resolution must be made. In order to help achieve the goal of high response speed (which is directly related to the number of bits used) and data resolution, we use logarithmic quantization, which has finer resolution near the desired equilibrium and coarser resolution farther from the equilibrium. Using this method allows us to get resolution as high as about +/- 10% of the total queue size using as few as 7 bits.
As can be inferred from the above discussion, stabilizing this network system is far from a simple task. In addition to the potentially non-linear dynamics of the system, one must also consider the delay inherent in the system, as well as the information limitations and the requirement to fairly share the available resources among all users. As a result this research is not only significant to the future of the Internet (and by extension to any highly distributed delay-sensitive system), it is also an interesting technical and theoretical challenge.

[1] H. Balakrishnan, N. Dukkipati, N. McKeown, and C.Tomlin, "Stability analysis of explicit congestion control protocols," http://sun-valley.stanford.edu/hybrid/, 2005.

[2] S. Deb and R. Srikant, "Global stability of congestion controllers for the internet," IEEE Trans. Autom. Contr., 6, pp. 1055-1060, 2003.

[3] L. Dugard and E. I. Verriest (Eds), Stability and Control of Time-Delay Systems, Great Britain: Springer-Verlag, 1998.

[4] A. Falk, D. Katabi, and Y. Pryadkin, "Specification for the explicit control protocol (XCP)," IETF Internet Draft, http://www.isi.edu/isi-xcp/docs/draft-falk-xcp-spec-01.txt, October 2005.

[5] E. Fridman and U. Shaked, "An improved stabilization method for linear time-delay systems," IEEE Trans. Autom. Contr., Vol 47, pp. 1931-1936, 2002.

[6] K. Gu, "Further Refinement of Discretized Lyapunov Functional Method for the Time-Delay Systems," in Proc. Amer. Contr. Conf., pp. 3998-4003, 2001.

[7] Y. Jing, M. Yang, G. Dimirovski, T. Ren, and Y. Zheng, "Global stability analysis about a congestion control scheme for networks with time delay," Proc. Amer. Cont. Conf, pp. 2399-2404, 2007.

[8] V. Jacobson, "Congestion avoidance and control," in Proc. ACM SIGCOMM, pp. 157-287, 1995.

[9] R. Johari and D. K. H. Tan, "End-to-end congestion control for the Internet: delays and stability," IEEE/ACM Trans. Netw, Vol 9, pp. 818-832, 2001.

[10] D. Kabati, M. Handley and C. Rohrs, "Congestion control for high bandwidth-delay product networks," Proc. ACM SIGCOMM, August 2002.

[11] L. Massoulié, "Stability of distributed congestion control with heterogeneous feedback delays," IEEE Trans. Autom. Contr., Vol 47, pp. 895-902, 2002.

[12] Y. Moon, P.Park, W. Kwon, and Y. Lee, "Delay-dependent robust stabilization of uncertain state-delayed systems," Int. J. Contr., Vol 74, pp. 1447-1455, 2001.

[13] F. Paganini, Z. Wang, J. Doyle, and S. Low, "Congestion control for high performance, stability and fairness in general networks," IEEE/ACM Trans. Netw, Vol 13, pp. 43-56, 2005.

[14] R. Srikant, The Mathematics of Internet Congestion Control, Boston: Birkhauser, 2004.

[15] T. Voice, "A global stability result for primal-dual congestion control algorithms with routing," ACM/SIGCOMM Comp. Comm., Vol 34, pp. 35-40, 2004.

[16] L. Ying, G. Dullerud, and R. Srikant, "Global stability of internet congestion controllers with heterogeneous delays," IEEE/ACM Trans. Netw, Vol 14, pp. 571-591, 2006.