Introduction
The research on option pricing of an option which holds more than one corporations' stocks had not been widely explored, because these types of option derivatives were very rare in the real financial world. This rarity of the option which holds two corporations' stocks can be explained by the principle of hedging. According to the principle of hedging, the necessary of an option derivative was to hedge the risk of investment by paying some amount of money to the party who is selling the option. Therefore, every corporation's stock could be hedged using different options and there was no need for considering an option holding more than one corporations' stocks.
On the other hand, in this busy world, financial organizations have started to realize the necessity of an option holding more than one corporations' stocks, to save the time and the amount of transactions. Therefore, the financial industries have started to explore on the problem of option pricing of an option holding more than one corporations' stocks [4].
Now, complex options which are dependent on multiple correlated stocks have become common in option pricing problems. These complex options are also called multi-dimensional options, where the number of dimension equals the number of stocks. Closed-form solutions to price such multi-dimensional options are available only in a few special cases, and hence numerical methods must be generally employed. A number of approaches have been proposed to numerically tackle option valuation problems. Broadly, these approaches can be divided into three types, namely, numerical methods to partial differential equations [1], Monte Carlo simulation methods [2], and lattice methods [3]. Among these, lattice methods are generally considered to be simpler and more flexible. Moreover, if the dimension of the lattice is not too large, the lattice method is more efficient than the others.
The BEG model by Boyle, Evnine, and Gibbs was the first lattice model, which handled more than one underlying stocks. When the BEG model was inherited from the CRR model developed by Cox, Ross, and Rubinstein, the BEG model adopted an unpleasant feature that the possibility of negative jump probabilities in the multi-dimensional lattice is high [3]. This is because the BEG model first sets the jump size, and then determines the jump probabilities.
Consequently, Ekvall (1996) introduced the NEK model, which was an extended model of the BEG model [4]. The NEK model has overcome the pitfall of the negative jump probabilities. Nevertheless, the NEK model has a problem of computational inefficiency in multi-dimensional option pricing.
Approach
Since the option price for an option holding two uncorrelated stocks can be analytically calculated, we focus on the case of an option holding two correlated stocks. In this research, we propose an efficient two-dimensional binomial (TDB) model as shown in Figure 1 to evaluate the option price, which holds two correlated stocks.
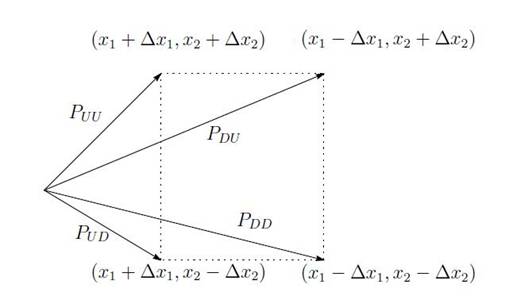
Figure 1: Two-Dimensional Binomial (TDB) Model
Figure 2 describes the total time to accomplish the option pricing calculation (option pricing time) versus the number of periods (n) in the models. According to Figure 2, it clearly shows that our proposed model is more efficient in option pricing calculation than the NEK model.
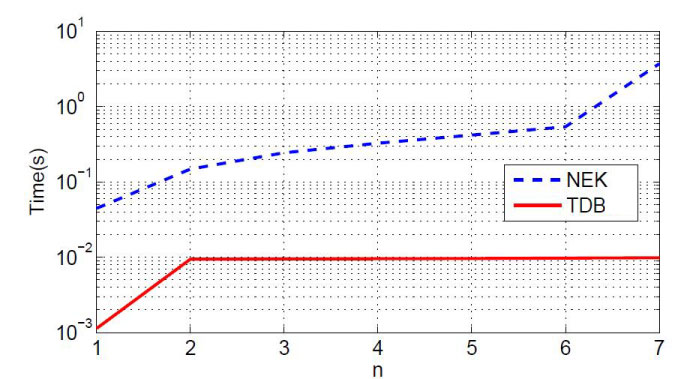
Figure 2: Option pricing time for TDB and NEK models
Finally, we provide another simulation result in Figure 3 to compare the option prices versus the number of periods in TDB model, NEK model, and analytical solution [5]. Though the TDB model is efficient than the NEK model, the TDB model’s price difference from the analytical solution is higher than the NEK model.
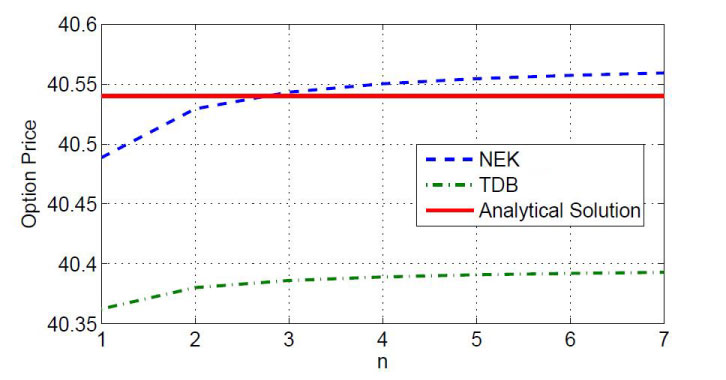
Figure 3: Option prices for TDBOP and NEK models
Results
To sum up, we have introduced an efficient option pricing model for options holding two correlated stocks. On the basis of the present results, our future research will focus on reducing the price difference from the analytical solution. Moreover, we will extend the TDB model for options holding more than two correlated stocks.
References
[1] M. Brennan and E. Schwartz, "The valuation of American put options,'' J. Fin., vol. 32, pp. 449-462, 1977.
[2] P. P. Boyle, "Options: a monte carlo approach,'' J. Fin. Econ., vol. 4, pp. 323–338, 1977.
[3] J. C. Cox, S. A. Ross, and M. Rubinstein, "Option pricing: a simplified approach,'' J. Fin. Econ., vol. 7, pp. 229–263, 1979.
[4] N. Ekvall, "A lattice approach for pricing of multivariate contingent claims,'' Eur. J. Oper. Res., vol. 91, pp. 214–228, 1996.
[5] H. Johnson, "Options on the maximum or the minimum of several assets,'' J. Fin. Quant. Anal., vol. 22, pp. 277–283, 1987.