2次元区分的アファインシステムのリミットサイクル解析と設計
情報環境学専攻 早川朋久研究室
修士課程2年 末永 昌也
■ 背景と目的
1. 非線形振動子ネットワークを用いた歩行制御
近年, 歩行ロボットの研究が数多く行われているが, その目的の一つに車輪では移動することの出来ない不整地歩行がある. 不整地歩行の実現のためには, 環境変化に対して適応的な歩行の実現が望まれるが, 実現されているロボットの多くは環境変化に対する適応性は低い. 一方, 動物は環境変化に対する適応性は高い. そこで, 動物の歩行制御メカニズムをロボットの歩行制御に適用させることにより, 環境変化等に対して適応的な歩行ロボットが実現可能であると考えられている.
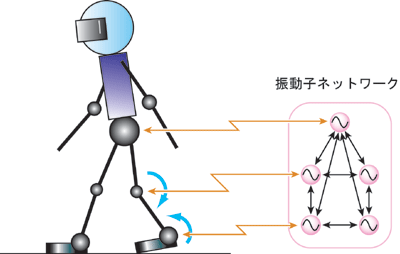
動物の歩行は, Central Pattern Generator(CPG)と呼ばれる神経回路により実現されていると言われている. CPGで生成された振動パターンが身体を駆動し, 身体からの環境の知覚情報がCPGへとフィードバックされることで安定な歩行を実現する[1](図 1).
CPGの振る舞いは数理上, 振動解を持つ非線形システムがネットワークの形で結合した非線形振動子ネットワークとして表現され, 近年では歩行ロボットへと応用されている. この歩行メカニズムをロボットに応用しようとする際, CPGの具体的な数理モデルを構築することが必要であるが, 明確な数理モデルは決まっていない. より解析や設計の容易な非線形振動子モデルを提案することは重要な課題である.
2. 既存の非線形振動子ネットワークモデル
非線形振動子ネットワークのモデルとして, Kuramotoモデル[2]やWilson-Cowanモデル[3], Matsuokaモデル[4,5]などが提案されている.
Kuramotoモデルは位相振動子モデルと呼ばれ, 振動子が1次元の状態量を持つ単純なモデルである. 近年では, Kuramotoモデルに基づいたネットワークの同期問題が盛んに研究されており, [2]では完全結合のネットワークを対象にしていたのに対し, [6,7]では, グラフ理論を用いることでネットワークが完全結合でない場合における同期条件を導いている.
Wilson-Cowanモデルは活性型ニューロンと抑制型ニューロンの2つが相互に結合したモデルである. 近年では, このモデルを修正し, 振動数, 振幅, 振動状態への収束度合いをパラメータとして持つ新しいモデルの提案が行われている[8]. このモデルは, 振動数, 振幅, 振動状態への収束度合いに関し, 所望のリミットサイクルを得ることが容易であるというメリットを持つ.
MatsuokaモデルもWilson-Cowanモデルと同様に活性型ニューロンと抑制型ニューロンの2つが相互に結合したモデルで表現されるが, Wilson-Cowanモデルとの違いは2点挙げられる. 1点目はWilson-Cowanモデルが2次元の振動子モデルであったのに対し, Matsuokaモデルは4次元のモデルであること, 2点目はWilson-Cowanモデルには非線形関数が陽に含まれるのに対し, Matsuokaモデルは区分的にアファインなシステムで表現されることである. つまり, MatsuokaモデルはWillson-Cowanモデルに比べて次元数が多いが, 単純なモデルであるといえる.
3. 非線形振動子を用いた歩行ロボット
非線形振動子を用いてロボットの歩行制御を実現させた例として, [9,10,11]がある. いずれもMatsuokaモデルを用いて構成された振動子ネットワークを用いており, 環境変化に対して高い適応性を持つ. ところが, 非線形振動子ネットワークとしてMatsuokaモデルを用いた歩行制御は, 適応性が高いという長所がある反面, パラメータの体系的な設定法が見つかっていないという問題を持つ. 文献[12,13]では強化学習や遺伝的アルゴリズムなどの学習アルゴリズムを用いたパラメータ決定法を提案しているが, パラメータの数が多いため, 学習が終了するまでに多くの試行回数を必要とする. したがって, 振動子ネットワークモデルの持つ内部パラメータを減らすなどのモデルの単純化が望まれている.
4. ハイブリッドシステムの平衡点解析
Matsuokaモデルのダイナミクスはハイブリッドシステムの一種である区分的アファインシステムとして表現される.
ハイブリッドシステムとは, ダイナミクスに離散変数と連続変数を持つシステムのことをいう. ハイブリッドシステムの中でも, 状態空間を区分的に領域分けを行い, 区分領域内ごとに線形システム, アファインシステムが定義されるシステムを区分的線形システム, 区分的アファインシステムという. 以下ではハイブリッドシステムの関連研究を紹介する.
現在までにハイブリッドシステムの平衡点に対する安定性についての研究は数多く行われている. 文献[14,15,16]では, 状態空間を放射状に区分した区分的線形システムに対し, 原点が指数安定となる必要十分条件が示されている. 文献[17,18]では, 区分的アファインシステムに対してリアプノフの手法を用いることにより, 平衡点の漸近安定条件を示している. 文献[19]ではポアンカレマップという考え方を導入し, [17,18]より保守性の低い条件を導出している. 文献[20]では平衡点の解析に加え, 区分的アファインシステムに対する制御問題も扱っている.
5. ハイブリッドシステムのリミットサイクル解析
状態空間上にある閉軌道を考える. このとき, システムの初期状態をこの閉軌道の近傍にとったとき, 状態軌道がこの閉軌道に漸近するとき, この閉軌道のことを安定なリミットサイクルという. ハイブリッドシステムが持つリミットサイクルの解析に関する研究も行われており, 文献[21]では, スイッチングシステムが持つリミットサイクルの大域的安定条件が提示されている. 文献[22,23,24,25]では, 区分的アファインシステムに対しポアンカレ写像の考えを用いることにより, リミットサイクルが漸近安定となる十分条件が示されている. さらに, 文献[26]ではより広いハイブリッドシステムのクラスに対するリミットサイクル解析手法を提示している.
このように, ハイブリッドシステムの持つリミットサイクルの安定性について数多くの研究がなされているが, いずれの研究でもリミットサイクルが存在するという仮定の下での安定性判別を行っている. 与えられたハイブリッドシステムがリミットサイクルを持つかどうかの判別手法を確立することには大きな意味がある. 滑らかな非線形システムがリミットサイクルを持つかどうかは, ポアンカレ-ベンディクソンの定理を用いて判別することができる[27]. 文献[28]によって, ポアンカレ-ベンディクソンの定理はハイブリッドシステムのような非連続なシステムに対して拡張されている. さらに, 与えられた滑らかな非線形システムに対し, リミットサイクルが存在しないことを判別する定理であるベンディクソンの定理をハイブリッドシステムに拡張する研究も行われている[29].
■ 研究目的
本研究の目的は, 解析や設計の容易な非線形振動子モデルを提案することにある. 本研究では, 2次元区分的アファインシステムを振動子として用いることを提案する. 2次元システムを考える理由としては, 振動子の次元数として2次元であれば十分であるとの考えである. なぜなら, 状態空間における閉軌道であるリミットサイクルは, ある非線形写像を用いることにより2次元空間に写像することが出来るためである. 一方, 区分的システムを用いる理由は位相によってシステムを調整するのが容易であることである. 例えば歩行制御において, 足を振る状態と, 足で支える状態に対して振動子の出力を調整をしたいという要求があるとする. その場合, 区分的システムであれば対応する状態空間における区分システムを調整することで対応できるためこのような要求に対応するのが容易である. アファインシステムを考えるのは, 区分的に1次のダイナミクスであり解析や設計がしやすい点にある.
■ 主結果
|
本研究では主に以下の3点について有効な結果を得ることができた. 簡単に紹介する. 1. 閉軌道の存在性解析[30]状態空間を放射状に区分する放射状2次元区分的アファインシステムを振動子として用いる際に, システムの解軌道が閉軌道を持つかどうかの判別を行うことは重要である. 本研究では放射状2次元区分的アファインシステムのパラメータが与えられた時に, システムが閉軌道を持つための条件の導出を行うことに成功した. 具体的には, 2次元非線形システムに対する閉軌道の存在定理であるポアンカレ・ベンディクソンの定理[27]と, 放射状2次元線形システムに対する解析手法を組み合わせることで結果の導出に成功した. 2. リミットサイクルの安定性・唯一性解析閉軌道が存在するだけでは, その閉軌道が安定なリミットサイクルかどうかの判別を行うことはできない. また, 安定なリミットサイクルが存在するだけではそのリミットサイクルがグローバルに安定かどうかを知ることはできない. そこで, 本研究では放射状2次元区分的アファインシステムが閉軌道を持つ時にその閉軌道が安定かつ唯一なリミットサイクルかどうかの判別を行う手法の提案を行った. ここでも, 放射状2次元線形システムの有用な結果を用いている. 3. リミットサイクル設計以上の結果を用いて, システムが安定なリミットサイクルを唯一に持ちつつ, 所望の振動波形をリミットサイクルとするような放射状2次元区分的アファインシステムのパラメータ設計法の提案を行った. 設計問題を拘束付き最適化問題とすることにより, 数値計算ソフトウェアを用いて容易に設計を行うことが可能である. 文献[31,32]において区分的アファインシステムのリミットサイクル設計問題が扱われているが, いずれも振動数, 振幅, 位相に関する設計問題を扱っており, より細かな波形の設計を行ってはいない. |
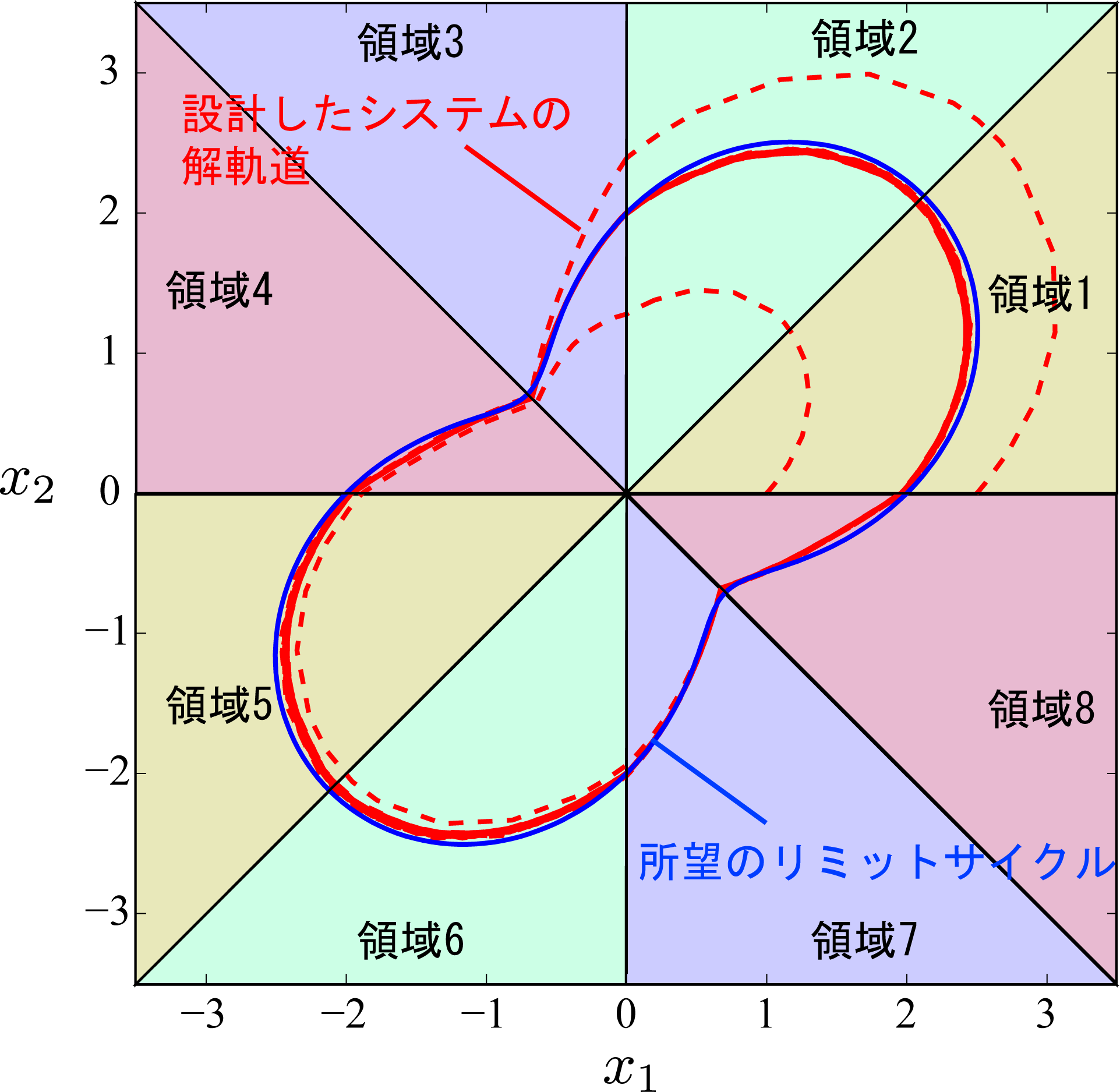
図 2 設計したシステムの軌道
|
■ これまでの結果と今後の課題
本研究では, 非線形振動子ネットワークの設計問題に対し, 所望の振動波形を実現する振動子設計問題を扱った. 今後の課題として, 本研究で提案した放射状2次元区分的アファインシステムをネットワークとして結合したときに, 個々の振動子の同期問題等を考えていくことが望まれる.
■ 参考文献
| [1] | 伊藤宏司, 身体知システム論 ―ヒューマンロボティクスによる運動の学習と制御. 共立出版, 2005. |
| [2] | 蔵本由紀, パターン形成. 朝倉書店, 1995. |
| [3] | H. R. Wilson and J. D. Cowan, ``Excitatory and inhibitory interactions in localized populations of model neurons,'' Biophys. J, vol. 12, pp. 1-24, 1972. |
| [4] | K. Matsuoka, ``Sustained oscillations generated by mutually inhibiting neurons with adaptation,'' Biol. Cybern., vol. 52, pp. 367-376, 1985. |
| [5] | K. Matsuoka, ``Mechanisms of frequency and pattern control in the neural rhythm generators,'' Biol. Cybern., vol. 56, pp. 345-353, 1987. |
| [6] | A. Jadbabaie, N. Motee, and M. Barahona, ``On the stability of the kuramoto model of coupled nonlinear oscillators,'' in Proc. Amer. Contr. Conf., (Boston, MA), pp. 4296-4301, July 2004. |
| [7] | N. Chopra and M. W. Spong, ``On synchronization of kuramoto oscillators,'' in Proc. IEEE Conf. Dec. Contr., (Seville, Spain), pp. 3916-3922, December 2005. |
| [8] | D. Zhang, D. Hu, L. Shen, and H. Xie, ``Dynamic analysis of a novel artificial neural oscillator,'' LECTURE NOTES IN COMPUTER SCIENCE, Springer, vol. 4491, pp. 1061-1068, 2007. |
| [9] | G. Taga, Y. Yamaguchi, and H. Shimizu, ``Self-organized control of bipedal locomotion by neural oscillators in unpredictable environment,'' Biol. Cybern., vol. 65, pp. 147-159, 1991. |
| [10] | 宮腰清一, 多賀厳太郎, 國吉康夫, 長久保晶彦, ``神経振動子を用いた三次元2足足踏みシミュレーション - ヒューマノイドの実世界内行動を目指して -,'' 日本ロボット学会誌, vol. 18, no. 1, pp. 87-93, 2000. |
| [11] | 福岡泰宏, 木村浩, ``4足ロボットの生物規範型不整地適応動的歩行 - 自立型「鉄犬2」による屋外歩行の実現 -,'' 日本ロボット学会, vol. 25, no. 1, pp. 138-154, 2007. |
| [12] | Y. Nakamura, T. Mori, and S. Ishii, ``Natural policy gradient reinforcement learning for a cpg control of a biped robot,'' Int. Conf. Parallel Problem Solving from Nature, pp. 972-981, 2004. |
| [13] | N. Sadati, ``Neural controller for a 5-link planar biped robot,'' IEEE Int. Conf. on Robot & Human Interactive Communication, pp. 980-985, 2007. |
| [14] | Y. Iwatani and S. Hara, ``Stability test based on eigenvalue loci for bimodal piecewise linear systems,'' in Proc. Amer. Contr. Conf., (Boston, MA), pp. 1879- 1884, July 2004. |
| [15] | Y. Iwatani and S. Hara, ``An exact stability test for planer and multi-modal piecewise linear systems,'' IFAC World Cong., 2005. |
| [16] | 西山聡史, 早川朋久, ``2次元区分的線形システムの切り替え面設計,'' 計測自動制御学会制御部門大会資料, 062-1-3, 京都, 2008. |
| [17] | R. A. Decarlo and M. S. Branicky, ``Perspectives and results on the stability and stabilizability of hybrid systems,'' Proc. IEEE, vol. 88, no. 7, pp. 1069-1082, July 2000. |
| [18] | M. Johansson and A. Rantzer, ``Computation of piecewise quadratic Lyapunov functions for hybrid systems,'' IEEE Trans. Autom. Contr., vol. 43, no. 4, pp. 555-559, 1998. |
| [19] | J. M. Goncalves, A. Megretski, and M. A. Dahleh, ``Global analysis of piecewise linear systems using impact maps and surface Lyapunov functions,'' IEEE Trans. Autom. Contr., vol. 48, no. 12, pp. 2089-2106, 2003. |
| [20] | A. Hassibi and S. Boyd, ``Quadratic stabilization and control of piecewise-linear systems,'' in Proc. Amer. Contr. Conf., (Philadelphia, PA), pp. 3659-3664, June 1998. |
| [21] | S. Varigonda and T. Georgiou, ``Global stability of periodic orbits in relay feedback systems,'' in Proc. IEEE Conf. Dec. Contr., (Sydney, Australia), pp. 3843-3847, December 2000. |
| [22] | M. Rubensson and B. Lennartson, ``Stability of limit cycles in hybrid systems using discrete-time Lyapunov tequniques,'' in Proc. IEEE Conf. Dec. Contr., (Sydney, Australia), pp. 1397-1402, December 2000. |
| [23] | M. Rubensson and B. Lennartson, ``Global convergence analysis for piecewise linear systems applied to limit cycles in a dc/dc converter,'' in Proc. Amer. Contr. Conf., (Anchorage, AK), pp. 1272- 1277, 2002. |
| [24] | 足立正和, 山本茂, 潮俊光, ``対称性を有する区分的アファインシステムにおけるリミットサイクルの解析,'' 電子情報通信学会論文誌 A, vol. J86-A, no. 3, pp. 207-212, 2003. |
| [25] | J. M. Goncalves, ``Regions of stability for limit cycle oscillations in piecewise linear systems,'' IEEE Trans. Autom. Contr., vol. 50, no. 11, pp. 1877-1882, 2005. |
| [26] | S. Pettersson and B. Lennartson, ``Exponential stability of hybrid systems using piecewise quadratic Lyapunov functions resulting in lmis,'' IFAC World Cong., 1999. |
| [27] | H. K. Khalil, Nonlinear Systems. Upper Saddle River: NJ: Prentice-Hall, 2002. |
| [28] | S. N. Simic, K. H. Johansson, J. Lygeros, and S. Sastry, ``Hybrid limit cycle and Hybrid Poincaré - Bendixson,'' IFAC World Cong., 2002. |
| [29] | A. Pogromsky, H. Nijsc.ejer, and J. Rooda, ``A negative bendixson-like criterion for a class of Hybrid systems,'' IEEE Trans. Autom. Contr., vol. 52, no. 4, pp. 586-595, 2007. |
| [30] | 末永昌也, 早川朋久, ``2次元区分的アファインシステムにおける周期軌道の存在条件,'' 計測自動制御学会制御部門大会資料, 062-1-1, 京都, 2008. |
| [31] | W. M. Lee and Y. Yam, ``Construction of central pattern generator using piecewise affine systems,'' in IEEE Int. Conf. Contr. Autom., (Guangzhou, China), pp. 1729-1734, May 2007. |
| [32] | Z. Chen and T. Iwasaki, ``Exact synthesis of biological pattern generation: a circuit paradigm,'' in Proc. Amer. Contr. Conf., (Minneapolis, MN), pp. 4112-4117, June 2006. |