背景
風力発電
再生可能なエネルギーに対する関心の高まりを一因として,世界的に風力発電システムの導入数は増加している.2020年までに世界の12%の電力が風力発電によって供給されるとの予測もなされている[1].日本では2010年に長崎県五島列島において国内最大規模の風力発電所(出力10万キロワット)運転開始が予定されている.一般的に原子力発電や火力発電に比べて,風力発電システムの発電コストが大きいと言われる.風力発電システムをより普及させるため,風力発電システムの発電効率を上げ,その発電コストを下げる技術の研究・開発が望まれている.
風力発電システム
風力発電システムのエネルギー変換
風力発電システムとは,風の持つエネルギーをブレードの回転エネルギーに変換し,それをさらに電気エネルギーに変換するシステムである.風の持つエネルギーからブレードの回転エネルギーへの変換は,風がブレードに当たるときにブレードに発生するトルクを通して行われる.風速が変動すると風がブレードに当たるときにブレードに発生するトルクが変動するのは自明であるが,ブレードに発生するトルクがタワーシャドウ効果によっても変動することが知られている.タワーシャドウ効果とはタワーに向かって吹く風がタワーの影響で減速するため,ブレードがタワーの前を通過するときに,ブレードが風から受けるトルクが小さくなる現象のことである.タワーシャドウ効果を起因としたトルクの変動は微小であるので,風力発電システムをモデル化するときに無視されることが多い.一方,ブレードの回転エネルギーから電気エネルギーへの変換は,シャフトに固定された界磁(以下,回転子)が励磁する磁界が回転し,発電機の中に固定された電磁石(以下,固定子)に起電力を発生させることを通して行われる.界磁は磁界を発生させるものであり,励磁した電磁石や永久磁石が使用される.このとき,回転子に流れる電流に,固定子の起電力により発生した磁界が作用することにより,シャフトに制動トルクが発生することになる.回転子が励磁する磁界の強さによって,固定子に発生する起電力の強さが変化し,同時にシャフトに発生する制動トルクも変化する.
風力発電システムの変換効率
風力発電システムにおいて風の持つエネルギーからブレードの回転エネルギーへの変換効率は,ある風速比(ブレード先端の速度と風速の比)で最大値を持つことが知られ,風の持つエネルギーからブレードの回転エネルギーへの変換効率を最大にする風速比は風車に固有の値となっている[2].つまり風の持つエネルギーからブレードの回転エネルギーへの変換効率を最大にするブレード回転角速度は風速の線形関数となる.風の持つエネルギーからブレードの回転エネルギーへの変換効率が最大値を持つ理由を簡単に説明すると次のようになる.1)ブレード回転角速度が風速によって決まる最適な角速度より大きくなると,ブレードに向かってくる風がブレードを避けてしまう傾向が増加し,ブレードが風から受けるトルクが減少する.その結果,風の持つエネルギーからブレードの回転エネルギーへの変換効率は減少する.一方,2)ブレード回転角速度が風速によって決まる最適な角速度より小さくなると,単位時間あたりにブレードが横切る面積が減少するために,ブレードが風から受けるトルクが減少する.その結果,風の持つエネルギーからブレードの回転エネルギーへの変換効率が減少する.以上2つの現象により,ブレードの回転角速度が風速によって決まる最適なブレードの回転角速度より大きくても小さくても,風の持つエネルギーからブレードの回転エネルギーへの変換効率が減少することになるので,風の持つエネルギーからブレードの回転エネルギーへの変換効率がある風速比で最大値を持つこととなる.
風力発電方式の分類
風車の運転方式はブレードの回転角速度に関して固定速運転方式と可変速運転方式の2つに大きく分けられる.これらの運転方式は,発電機の出力の周波数を電力の供給先である電力系統の系統周波数に常に合わせることができるように設計されている.固定速運転方式はブレードのピッチ角(ブレードの取り付け角度)を操作することで風速に関わらず一定のブレード回転角速度を維持する方式である.ブレード回転角速度を一定に保つことで,発電機の出力の周波数を電力の供給先である電力系統の系統周波数に常に合わせることができる.固定速運転方式の風力発電システムでは,ある値の風速においてのみ,風の持つエネルギーからブレードの回転エネルギーへの変換効率を最大にすることができる.
一方,可変速運転方式はブレード回転角速度を変速させながら運転する方式である.可変速運転方式に用いられる発電機として代表的な同期発電機では,外部電力や永久磁石で励磁された回転子が励磁する回転磁界により,固定子に起電力を生じることで発電をする.このときシャフトの回転数に対応した周波数の交流電力を発電するので,シャフトの回転数に応じて発電周波数が変わることになる.ブレード回転角速度の可変速運転が可能な理由は,インバーター・コンバーターを用いて,発電機の出力を一度直流に変換し再び交流に戻すことで,発電周波数を系統周波数に合わせることが可能であるからである.このとき回転子と固定子が磁場で相互作用することによってシャフトに制動トルクが発生し,その制動トルクと風がブレードに当たるときにブレードに発生するトルクの差によってブレードの回転角速度が変化する.ここで,外部電力から回転子に加える電圧によってシャフトに発生する制動トルクが変化し,結果としてブレードの回転角速度が変化することになる.
可変速運転方は市場において主流である風車の運転方式である.その理由の一つは,風速に合わせてブレード角速度を制御をすることで,一定の範囲の風速において風の持つエネルギーからブレードの回転エネルギーへの変換効率を最大に近くすることが可能であるためである.ここで一定の範囲の風速とは,発電が可能である最小の風速からその風速のとき発電が可能である最大の発電電力が発電機の定格(最大)出力に達するまでの風速を表す.風速が増加し発電電力が発電機の定格出力に達すると,その定格を超えないように出力制限を行い,さらに風速が増加し,風車に決められた最大風速を超えた場合,風車が壊れるのを防ぐために風車の運転を停止することになる.ここで発電を開始できる風速から発電出力に達する風速までの間,風の持つエネルギーからブレードの回転エネルギーへの変換効率を最大化するよう風力発電システムを制御することを部分負荷運転をするという.
先行研究
風力発電システムの出力最適化のための制御
可変速運転方式の風力発電システムにおける部分負荷運転で望まれることは発電効率を最大化し,同時に風車にかかる機械的な負荷を減らすことである.一般的に,ブレードの回転エネルギーから電気エネルギーへの変換効率は常に一定もしくはその変動が無視できるぐらい小さいと仮定することが多い[3].このとき風力発電システムにおいて発電効率を最大化することと,風の持つエネルギーからブレードの回転エネルギーへの変換効率を最大にすることは等価となる.風速が急激に変化したとき,風の持つエネルギーからブレードの回転エネルギーへの変換効率を維持するためにブレード回転角速度を風速に合わせて急激に変化させようとすると,慣性の大きいブレードを駆動するためにシャフトに大きなトルクを発生させる必要がある.これは結果的に機械的な負荷をシャフトやブレードにかけることになるので,発電効率の最大化と風車にかかる機械的な負荷を減らすことを両立する制御は簡単ではない.
可変速運転方式の部分負荷運転において,様々な制御手法(LQ制御[4],LQG制御[5,6],QFT制御[7,8],LMI制御[9])が提案されているが,上記の制御方式の多くは風速が計測できることを想定している.しかし,商用の実際の風力発電システムにおいて風速情報をコントローラにフィードバックしているものはそれほど多くない.MW級の風力発電システムになるとブレードの半径も巨大(数十メートル)になるが,ブレード全体にどのような風が吹いているかを計測するのは困難である.そこでブレードを大きな風速計であるとみなし,カルマンフィルタを用いて風速を推定している手法も提案されている[10].風速の正確な推定を行うためにはシステムのパラメータについて正確な情報が必要となる.一方,システムについての最小限の情報で出力最適を目指す方法も提案されており,最大点追従(Maximum Power Point Tracking:以下,MPPT)と呼ばれるものである.
風力発電システムにおけるMPPT
風力発電システムにおける可変速運転方式の部分負荷運転におけるMPPTの研究は,一般的に次の問題設定で行われている.風の持つエネルギーからブレードの回転エネルギーへの変換効率を最大にする風速比は未知であり,発電機の定格出力,定格角速度,シャフトとブレードの慣性モーメントは既知であるとする.また,風速は測定できないとし,ブレード回転角速度と発電機の出力は計測可能であるとする.この問題設定において風力発電システムの出力とブレード回転角速度の関係を多項式で推定[11],またはニューラルネットで推定[12]することで最適なブレード回転角速度を求める手法が提案されている.これらの手法は有用であるが,著者の知る限りブレード角速度の最適値への収束性の保証は理論的に行われていない.一方,山登り法(Hill-climbing method)を基本的なアイデアとしたMPPTも提案されており[2,13,14],特に[2]で提案された手法はブレード角速度の最適値への収束性の理論的解析がなされている[15].山登り法とは,過去の出力と現在の出力を比べてより大きい出力を与える入力を最適な入力とする手法である.シンプルな手法であるが,ブレード角速度の最適値への収束スピードはあまり速くない.
風力発電システムにおける極値制御
山登り法に比べブレード角速度の最適値への収束スピードの改善が期待でき,ブレード角速度の最適値への収束の解析[16]が行われている,極値制御(extremum seeking control)を用いたMPPTも提案されている[3,17].極値制御手法とは,不確かさを持つシステムの入力に周期的な外生信号を加え,システムの出力のうち入力に加えた周期的な外生信号と同じ周波数の成分の位相と外生信号の位相を比べることで,出力を最大化する最適な入力値に比べて現在の入力値が大きいか小さいかの情報を得ることができるというアイデアに基づいた手法である.最適な入力値に比べて現在の入力値が大きいか小さいかという情報を用いて,現在の入力値を最適な入力値があると思われる方向に近づけていくことにより出力を最大化できる.文献[16]で提案された極値制御を用いて,風の持つエネルギーからブレードの回転エネルギーへの変換効率の最大化を行う手法[17]では,入力に周期的な外生信号を加え制御系を構築しているが,これはブレードにかかるトルクを高周波で変動させることとなり,機械的な負荷を増加させる原因となると考えられる.一方,入力に加える周期的な外生信号の代わりに,実際の風の変動を用いて極値制御を行う手法[3]では,コントローラの設計に風速の正確な計測が必要である.
アプローチ
風力発電機の出力最大化制御
本研究では,極値制御を用いた可変速運転方式の風力発電システムでの部分負荷運転時における風の持つエネルギーからブレードの回転エネルギーへの変換効率の最大化を考える.既存の極値制御を用いた手法[3,17]において問題であった,ブレードにかかるトルクを高周波で変動させること,風速の正確に計測することの両方を必要としない手法を提案する.本研究の提案手法では入力に加える周期的な外生信号の代わりとして,風力発電システムに既に存在するタワーシャドウ効果を用いる.実際の風の変動を用いて極値制御を行う手法[3]では,風力発電システムをタワーシャドウ効果を考慮せずモデル化していた.これはタワーシャドウ効果がシステムに与える影響が非常に小さいためであるが,極値制御を行う場合,周期的な変動をシステムに与えるタワーシャドウ効果は,入力に加える周期的な外生信号の代わりとして用いることができる可能性がある.さらにタワーシャドウ効果はブレードがタワーの前を通過するときに発生するので,ブレードの位相により発生タイミングを知ることができ,風速の正確な情報がない状況でも,ブレードの位相情報を用いることで極値制御系を構築できる利点がある.さらに,入力に周期的な外生信号を加えることなく,風力発電システムに既に存在する変動を用いることでブレードに加わる機械的な負担の軽減を期待できる.
結果
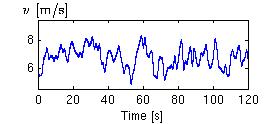

シミュレーション結果
本研究で提案したタワーシャドウ効果を用いた極値制御手法の数値実験を行った.風力発電システムは[18]の小型(6kW)風力発電システムとした.また,シミュレーションに用いる小型風力発電システムの変換効率の最大値は0.47629である.図1の横軸は時刻[s]を表し,縦軸は風速v[m/s]を表す. 図2の横軸は時刻[s]を表し,縦軸は変換効率Cpを表す. この結果より,変換効率は最大値に収束傾向にあることがわかる.
結論
本研究では,タワーシャドウ効果を外生信号の代わりに用いた極値制御による可変速運転方式の風力発電システムの部分負荷運転における風のエネルギーからブレードの回転エネルギーへの変換効率の最大化を提案した.タワーシャドウ効果を用いることで,既存研究に比べ,極値制御系の構築に風速の正確な計測を必要とせず,ブレードを高周波で振動させることのない利点があった.また,シミュレーションにより提案手法の有効性の検証を行った.今後の課題は,風速が短期的に変動する場合において,極値制御を行った風力発電システムの閉ループ系の安定性を解析を行うことである.
参考文献
| [1] | Global Wind Energy Council, ``Wind Force 12,'' Tech. Rep., Greepeace Ed, 2005. |
| [2] | K. E. Johnson, L. J. Fingersh, M. Balas, and L. Y. Pao, ``Methods for increasing region 2 power capture on a variable speed HAWT,'' in Proc. ASME Wind Energy Symposium, (Reno, NV), pp. 103-113, 2004. |
| [3] | I. Munteanu, A. I. Bratcu, and E. Ceanga, ``Wind turbulence used as searching signal for MPPT in variable-speed wind energy conversion systems,'' Renewable Energy, 2009. |
| [4] | E. S. Abdin and W. Xu, ``Control design and dynamic performance analysis of a windturbine-induction generator unit,'' IEEE Trans. Energy Conv., vol. 15, no. 1, pp. 91-96, 2000. |
| [5] | P. Novak, T. Ekelund, I. Jovik, and B. Schmidtbauer, ``Modeling and control of variable-speed wind-turbine drive-systemdynamics,'' IEEE Contr. Syst. Mag., vol. 15, no. 4, pp. 28-38, 1995. |
| [6] | E. B. Muhando, T. Senjyu, A. Yona, H. Kinjo, and T. Funabashi, ``Regulation of WTG dynamic response to parameter variations of analytic wind stochasticity,'' Wind Energy, vol. 11, no. 2, pp. 133-150, 2008. |
| [7] | N. A. Cutululis, E. Ceanga, A. D. Hansen, and P. Sorensen, ``Robust multi-model control of an autonomous wind power system,'' Wind Energy, vol. 9, no. 5, pp. 399-419, 2006. |
| [8] | E. Torres and M. Garcia-Sanz, ``Experimental results of the variable speed, direct drive multipole synchronous wind turbine TWT 1650,'' Wind Energy, vol. 7, no. 2, pp. 109-118, 2004. |
| [9] | F. D. Bianchi, R. J. Mantz, and C. F. Christiansen, ``Gain scheduling control of variable-speed wind energy conversion systems using quasi-LPV models,'' Control Engineering Practice, vol. 13, no. 2, pp. 247-255, 2005. |
| [10] | N. Kodama, T. Matsuzaka, and N. Inomata, ``The power variation control of a wind generator by using probabilistic optimal control,'' Trans. Inst. Elect. Eng., vol. 121-B, no. 1, pp. 22-30, 2001. |
| [11] | S. Bhowmik, R. Spee, and J. H. R. Enslin, ``Performance optimization for doubly fed wind power generationsystems,'' IEEE Trans. Ind. Appl., vol. 35, no. 4, pp. 949-958, 1999. |
| [12] | H. Li, K. L. Shi, and P. G. McLaren, ``Neural-network-based sensorless maximum wind energy capture with compensated power coefficient,'' IEEE Trans. Ind. Appl., vol. 41, no. 6, pp. 1548-1556, 2005. |
| [13] | R. Datta and V. T. Ranganathan, ``A method of tracking the peak power points for a variable speed wind energy conversion system,'' IEEE Trans. Energy Conv., vol. 18, no. 1, pp. 163-168, 2003. |
| [14] | Q. Wang and L. Chang, ``An intelligent maximum power extraction algorithm for inverter-based variable speed wind turbine systems,'' IEEE Trans. Power Electron., vol. 19, no. 5, pp. 1242-1249, 2004. |
| [15] | K. E. Johnson, L. Y. Pao, M. J. Balas, V. Kulkami, and L. J. Fingersh, ``Stability analysis of an adaptive torque controller for variable speed wind turbines,'' in Proc. IEEE Conf. Dec. Contr., (Paradise Island, Bahamas), pp. 4087-4094, 2004. |
| [16] | M. Krstic and H. H. Wang, ``Stability of extremum seeking feedback for general nonlinear dynamic systems,'' Automatica, vol. 36, pp. 595-601, 2000. |
| [17] | M. Komatsu, H. Miyamoto, H. Ohmori, and A. Sano, ``Output maximization control of wind turbine based on extremumcontrol strategy,'' in Proc. Amer. Contr. Conf., (Arlington, VA), pp. 1739-1740, 2001. |
| [18] | I. Munteanu, A. I. Bratcu, N.-A. Cutululis, and E. Ceanga, Optimal Control of Wind Energy Systems: Towards a Global Approach. newblock Springer, 2008. |