システムの状態空間がいくつかの領域に区切られており, 各領域で別々の線形ダイナミクスを有するようなシステムのことを区分的線形システムという. この各領域の区切り方をうまく選んでやることで, 不安定な固有値を持つサブシステムの組み合わせを１つの安定なダイナミクスとすることができる. ２次元の場合ではこの切り替え面の選び方は[1]で提案されている. また, 規則的な切り替え法則を持つケースについて, スイッチするそれぞれのシステムの固有値に基づいた安定性判別の方法が[2]で提案されている.
　より一般的な切り替えを持つ switching system の安定性について, [3]で dwell-time と chatter bound という２つのパラメータを用いて議論されている. ここでは, ある条件を満たすような dwell-time と chatter bound を持つ切り替えシステムについて, 安定性判別法が提案されている. 文献[4]においては,特定の(※1)サブシステムを持つ switching system について, サブシステム全てが漸近安定である事が switching system が漸近安定である事の必要十分条件である事が述べられている.
　これらの方法では, 安定となるように切り替え方法を設計したり, あらかじめ切り替えの方法を設定したりしているため, 不規則なシステムの切り替えが起こるようなものに適用できない. そこで, 不規則なダイナミクスの切り替えを持つ switching system の安定性について研究を行う.
(※1, ここでは全てのサブシステムがお互いに可換であるという条件を設定している)

■ シミュレーション

　切り替えがあるとき, 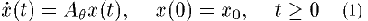で表されるような switching system を考える. ただし, 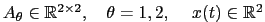とする. このとき, switching system に関する行列(※2)の固有値からシステムの安定性を議論できるのか, 可能性を検討するため,以下のようなシミュレーションを行った.
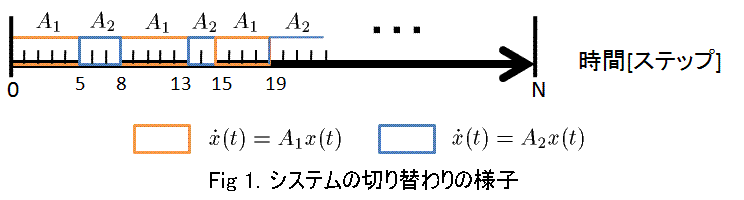
　今回のシミュレーションでは, 初期条件としてt=0でθ=1とする. システムの切り替えは, １ステップ(τ)毎にしか起こらないものとして, そしてある時刻(nステップ目)でθ=1 である確率を p として与える. この p の値を変えながらシミュレーションを行った. A1, A2行列に, 安定なもの(固有値の実部が負のみ), 不安定なもの(固有値の実部に正の数を持つ)の両方を用い, 組み合わせを変えながらシミュレーションを行った.

(※2 今回はAθの期待値となる行列の固有値を考えた)



　 今回行ったシミュレーションでは以下のような結果を得た.

1. A1,A2が２つとも安定な行列であるならば, p の値に依らず(1)の状態変数は0に近づいていく.
2. A1,A2が２つとも不安定な行列であるならば, p の値に依らず(1)の状態変数は大きくなっていく.
3. A1,A2のうち片方が安定でもう片方が不安定な行列であるならば, (1)は p の値に依って変化する.

シミュレーション結果を踏まえ, (1)で表わされるような switching system が２乗モーメント安定であるかを検討する. 今回のシミュレーションではτ毎にしかシステムの切り替えが発生しないと仮定したが, そうでない任意の時間にシステムの切り替えが起こるシステムを考える.

■ 参考文献

[1]	西山聡史, "２次元区分的線形システムの切り替え面設計," 平成18年度東京工業大学学士論文, 2007.
[2]	岩谷靖, 原辰次,"固有値に着目した２モード区分的線形システムの安定解析," 計測自動制御学会論文集, vol. 39, no. 11, pp. 1048-1053, 2003.
[3]	W. Feng, and J. Zhang,"Stability analysis and stabilization control of multi-variable switched stochastic systems," Automatica, vol. 42, no. 1, pp. 169-176, 2006.
[4]	H. Lin, and P. J. Antsaklis,"Stability and stabilizability of switched linear systems: A short survey of recent results," in Proc. IEEE Int. Symposium on Intelligent Control, (Limassol, Cyprus), pp. 24-29, June 2005.