状態制約最適インパルス制御問題と
投薬スケジューリングへの応用
関根亮二
|
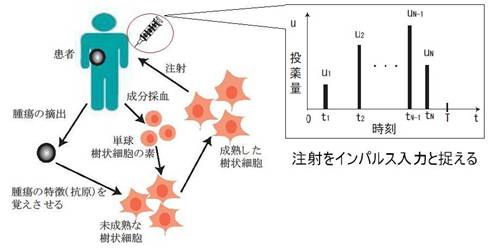
はじめに 現在日本人の最も多い死亡原因は癌であり,平成15 年の全死亡者に占める割合は30.5 %である[5].多くの人が死に至る病である癌の治療方法の一つに免疫細胞療法がある.免疫細胞療法とは,体内に存在する免疫力を高めることで癌の増殖を抑えることや,外科手術後の癌の転移・再発を抑えることを目的とした治療法である[9].この免疫細胞療法の一つである樹状細胞療法は,図1で表されるように,患者自身の腫瘍細胞の蛋白質を患者から取り出した樹状細胞に取り込ませるか,腫瘍細胞の抗原が解析されている場合はその腫瘍細胞の抗原ペプチドを生成し,患者から取り出した樹状細胞と結合させることによって腫瘍細胞の抗原をその樹状細胞に覚えさせ,注射などの方法で患者の体内に樹状細胞を注入する方法で行われる[9].体内に戻された樹状細胞は腫瘍細胞の抗原をリンパ球に提示し,攻撃対象を覚えたリンパ球は体内を循環し,腫瘍細胞を攻撃する. 樹状細胞療法の投薬スケジューリング問題を制御工学的な視点で捉えた場合,制御目標は腫瘍細胞の数を正常の値にまで減らすことであり,投薬量を増やすほど腫瘍細胞の数を減らすことができると予想される.しかし,患者自身の体から薬の材料を取り出すという樹状細胞療法の性質上,投薬量を増やすことによる患者の体への負担の増加が見込まれるので,投薬量も少ない方が良い.よって,制御目標はなるべく少ない投薬量で腫瘍細胞の数を正常の値にすることである.また,樹状細胞の注入を入力と考え,この入力は免疫系のタイムスケールに比べて瞬間的なものと見ることができ[1],インパルス入力とみなすことができる.さらに,転移の危険性や他の細胞へ深刻な影響を与える可能性があることなどの理由により,治療期間における腫瘍細胞の数に上限を設ける必要があり,これを状態制約と捉えることができる.そこで,本研究では樹状細胞療法の投薬スケジューリング問題の最適解を求めることを動機として,この問題を状態制約最適インパルス制御問題として一般化して捉え,最適な入力スケジュールを求める手法を提案することを目的とする.
図1: 樹状細胞療法とインパルス入力 先行研究 文献[3,4]では,インパルス入力と連続的な入力を併用する問題設定の最適インパルス制御問題における評価関数のインパルス入力ベクトルに関する勾配を導いている.また,[1,2]ではインパルス入力のみを使う最適インパルス制御問題におけるインパルス入力時刻に関する評価関数の偏微分を,[1]ではさらにインパルス入力ベクトルに関する評価関数の勾配を導いている.しかし,評価関数の各時刻における入力ベクトルと入力時刻に関する勾配だけでは状態制約を扱うことができない.そこで,文献[1]では状態制約最適インパルス制御問題に対し,状態制約を満たす場合には0,状態制約を満たさない場合には正の値を持つ罰則関数を評価関数に組み込み,状態制約最適インパルス制御問題を無制約最適インパルス制御問題に変換し,最適な入力スケジュールを求める方法で状態制約を実現しようとしている.しかし,この方法は罰則関数に対する重みが固定であること以外は外点ペナルティ法(罰則関数に対する重みを変化させて無制約最適制御問題を繰り返し解く)と同様の手法であるため,罰則関数に対する重みが小さい場合,状態制約を満たさないことがある点と,逆に罰則関数に対する重みが大きすぎる場合,数値的に不安定になるという点で,外点ペナルティ法と同様の問題点がある[6]. アプローチ 本研究では,状態制約最適インパルス制御問題において,状態制約最適制御問題を不等式制約最適化問題に変換することで,状態制約を扱う.文献[7,8]では,時間に関して連続な入力を加える状態制約最適制御問題に対し,状態制約非線形計画問題の局所最適解の必要十分条件であるKarush-Kuhn-Tucker
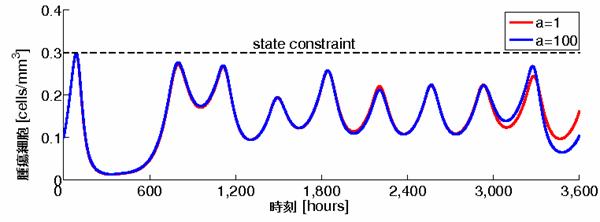
条件の式の解を準Newton 法で探索する手法(逐次2次計画法[6])を利用している.逐次2次計画法は非線形計画法の一つなので,状態制約最適制御問題に対して利用するために関数空間を利用して,状態制約最適制御問題を不等式制約最適化問題に変換している.本研究では,この手法を応用し,逐次2次計画法を利用した状態制約最適インパルス制御問題の解法を導く. 結果 前節で提案する手法を用いて,はじめに述べた樹状細胞療法の投薬スケジューリング問題を解き,本手法の有効性を示す.樹状細胞療法における免疫細胞のダイナミクスは文献[2]のモデルを使用する.投薬回数は10回とし,終端時刻を3600[h](150日)とし,単位体積当たりの腫瘍細胞の数の上限を0.3[cells/mm3]とする.評価関数は終端時刻における単位体積当たりの腫瘍細胞の数の二乗に重み定数aをかけたものと,樹状細胞の各投薬時刻における投薬量の二乗との和とする.図2に重みaが1と100のときのシミュレーション結果を示す.
図2: 異なる重みを用いたときの単位体積当たりの腫瘍細胞の数の軌道 終端時刻における単位体積当たりの腫瘍細胞の数に注目すると,重みaが大きいほうが小さい値になっていることが分かる.これは評価関数の局所的な最小値を求めることに成功していることを意味している.また,単位体積当たりの腫瘍細胞の数の軌道に注目すると,どちらの重みについても制約条件を満たしていることがわかる.したがって,本研究の手法が有効であるといえる. 参考文献 [1] F. Castiglione
and B. Piccoli, ``Optimal control in a model of dendritic cell transfection
cancer immunotherapy,'' Bull. Math.
Biol., vol. 68, no. 2, pp. 255--274, 2004. [2] F. Castiglione
and B. Piccoli, ``Cancer immunotherapy,
mathematical modeling and optimal control,'' J. Theor. Biol., vol. 247, pp. 723-732,
2007. F. Castiglione
and B.\ Piccoli, ``Optimal control in a model of dendritic cell transfection
cancer immunotherapy,'' in Proc. IEEE
Conf. Dec. Contr., ( [3] J. Chudoung
and C. Beck, ``The minimum principle for deterministic impulsive control
systems,'' in Proc. IEEE Conf. Dec.
Contr., ( [5] 厚生労働省ホームページ(http://www.mhlw.go.jp/index.html). [6] 坂和正敏,
``非線形システムの最適化<一目的から多目的へ>,'' 森北出版, 1986. [7] 志水清孝,
伊藤聡,``Hilbert
空間における双対準
Newton 法とその状態制約最適制御問題への応用,'' 計測自動制御学会論文集, vol. 26, no. 9, pp. 1025-1022, 1990. [8] 志水清孝,
``最適制御の理論と計算法,'' コロナ社, 1994. [9] 日本免疫治療学研究会(http://www.jrai.gr.jp/index.html). Tokyo
Institute of Technology Dynamical
Systems Lab 平成20年3月24日更新 |