金融工学，特に資産運用においては，リスクを少なく抑えることや，最適な運用を行うことの必要性が存在する． そのため，対象をモデル化し，必要な入力を加え，所望する結果をもたらすという制御のメソッドが有効であると考えられる． 本研究では，確率システムの制御という観点で資産運用手法を提案し，その成果の定量的評価を行うことを目的とする．

　ポートフォリオ最適化問題とは，いくつかの資産の組み合わせによりリスクを小さく抑えつつ，リターンが大きくなるような ポートフォリオ構成を求めることである．初めてリスクを定量的に扱い，理論的なモデルを構築し，そのモデル上での最適な解を導いたのが ハリー・マーコヴィッツであった[1]．マーコヴィッツは価格が確率的に変動する複数の資産の最適な保有比率を，それぞれの収益率の平均と分散を用いた 条件付極値問題に帰着して導出した．この研究を先駆けに，ウィリアム・シャープ[2]やジョン・リンター[3]らがそれぞれ独自にCAPM （資本資産価格モデル）と呼ばれる実用的な手法を開発し，実務家の間でも用いられるようになった．マーコヴィッツとシャープはこの功績で ノーベル経済学賞を受賞している．
　ポートフォリオ最適化問題の研究はその後も主にOR（Operations Research)の分野で行われており，より現実的な，取引コストを含む モデルに対し，非凸型最適化問題や多期間最適化問題へのアプローチ手法を応用した研究が行われている．また，大規模最適化問題など高い計算機能力を要する 問題を実用的に解くための効率的なアルゴリズムの開発など計算機科学的アプローチもなされている[4]．

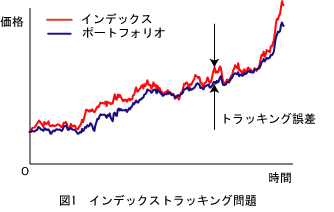
　インデックスとは，日経平均株価や東証株価指数（TOPIX）など，株式市場の平均的動きを表す指標の総称である．そして，インデックス運用とは ，ポートフォリオの価格の変動を，目標とするインデックスの変動に追従(トラッキング)させるような資産運用手法である． このような資産運用手法が金融業界に初めてあらわれたのは1970年代のアメリカであった． いわゆる市場の平均の動きであるインデックスと同じ資産運用成果を目指すことは，実証研究においてその有効性が示されてはいたが[5]， その誕生直後にあってはあまり投資家の注目を得ることができなかった．しかし，その有効性は徐々に一般に認知されてゆき，現在においては巨大な市場規模を持つに至っている．
　理想的なインデックス運用は，原理的に，インデックスの構成要素となるすべての株式をポートフォリオに組み込むことで実現できるのであるが，インデックスを構成する株式の種類が 多い場合，それらすべての株式をポートフォリオに組み込むには巨額の資産が必要となり，大規模なファンドにしか実現することができないのが普通である．そこで，少額の資産 でインデックス運用を行うために，ポートフォリオに組み込む株の種類を少なくする手法がとられている．しかし，この手法では，図1に示すようなインデックスとポートフォリオ の価格の誤差である，トラッキング誤差が生じてしまう． このトラッキング誤差を最小にするポートフォリオを構成する問題をインデックストラッキング問題という．

　ポートフォリオ最適化問題はその親和性からORの分野での研究が多勢を占めているが，長い制御理論の研究で培われた手法の適用が今後期待されている[6]． 実際に[7]では，最適ポートフォリオ問題を最適制御問題に置き換え，ハミルトン・ヤコビ・ベルマン方程式と呼ばれる偏微分方程式を解く問題に帰着させている． 文献[8]では，株価の価格変動を確率過程としてモデル化し，インデックストラッキング問題を確率システムの制御の一種であるSLQ（Stochastic Linear Quadratic）制御問題 に帰着している．しかしその際，リカッチ方程式を用いた解の導出法は適用できないため，半正定値計画問題として解く手法を提案している．文献[9]では，モデル予測制御 (MPC)を用いて，ポートフォリオのリスクの度合いを表すVaR(Value at Risk)という指標を一定値以下に抑えるという拘束条件の下，利益を最大化するポートフォリオを導出している．

　本研究では，インデックストラッキング問題に対して，資産運用を制御入力とみなし適切な制御を行い，トラッキング誤差の特徴付けを行うことを目的とする． ここで，トラッキング誤差の特徴付けとは，原理的にトラッキング誤差を0に制御することは不可能であっても，ある制御を行えば，ある範囲内にトラッキング誤差が 収まるといったようなトラッキング誤差の振る舞いの特徴をとらえることである．その際，トラッキング誤差や株価を状態量として持つ確率システムとして インデックストラッキングモデルを導出し，このモデルの安定性解析を行うことでトラッキング誤差の特徴付けを行う．しかし，株価は安定な状態量ではないため， モデルが持つすべての状態量の安定性を扱う通常の安定性解析手法は用いる ことができない．そこで，状態量の一部分に限定した安定性解析を行うことができる非線形システムの安定性解析手法である部分安定性理論[10]を用いる．

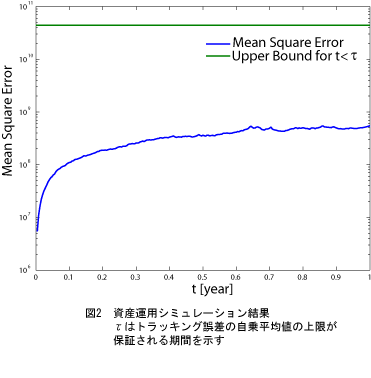
　本研究では，資産運用に利用できる銘柄数がインデックスを構成する銘柄数よりも少ない際に生じてしまうトラッキング誤差を特 徴づけるという目的のもと，トラッキング誤差が従うダイナミクスを確率微分方程式でモデル 化し，その安定性解析を行うことで，トラッキング誤差の自乗平均値を一定値以下に抑えることが保証される資産運用手法と，その手法が存在するための十分条件を導出した． この条件は資産運用に利用することのできる株式の株価変動モデルが持つパラメータによって導出さ れる．そのため，資産運用に利用する株式の選定の際，条件がより満たされやすいように選ぶ ための指標を各株式の株価変動モデルのパラメータに見出すことができる． 実際に，この運用手法のシミュレーションを行った結果を図2に示す．これより，トラッキング誤差の自乗平均値を一定値以下に抑えることができていることがわかる．
　今後の課題としては，株式の購入に時間遅れを考慮することや，株式の売買コストを組み込 んだシステムを制御対象にすることなど，より現実的なモデルを扱うことが考えられる．